Aufgabe:
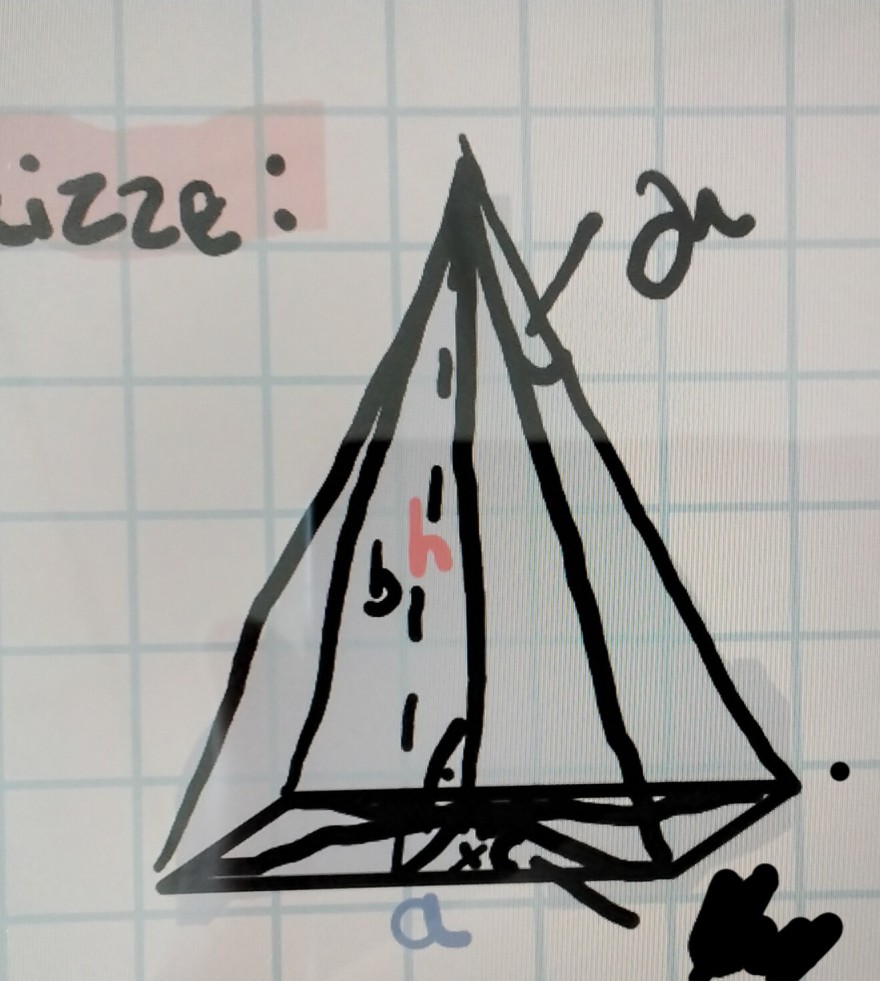
Die Spitze eines Kirchturms har die Form einer regelmäßigen quadratischen Pyramide mit der Grundseite a=7,20m und der Höhe h=13,60m.
a.)Berechne den Neigungswinkel α der Seitenflächen gegenüber der Grundfläche.
b.)Berechne den Öffnungswinkel γ an der Turmspitze, der von zwei gegenüberliegenden Kanten eingeschlossen wird.
c.) Berechne den Flächeninhalt des Daches
Problem/Ansatz:
Wie berechnet man den Neigungswinkel und den Öffnungswinkel und den Flächeinhalt?