Hallo,
bilde die 1. Ableitung, setze sie gleich 0 und löse nach x auf.
Prüfe dann mit Hilfe der 2. Ableitung oder einer Vorzeichentabelle, ob es sich um einen Hoch- oder Tiefpunkt handelt.
a)
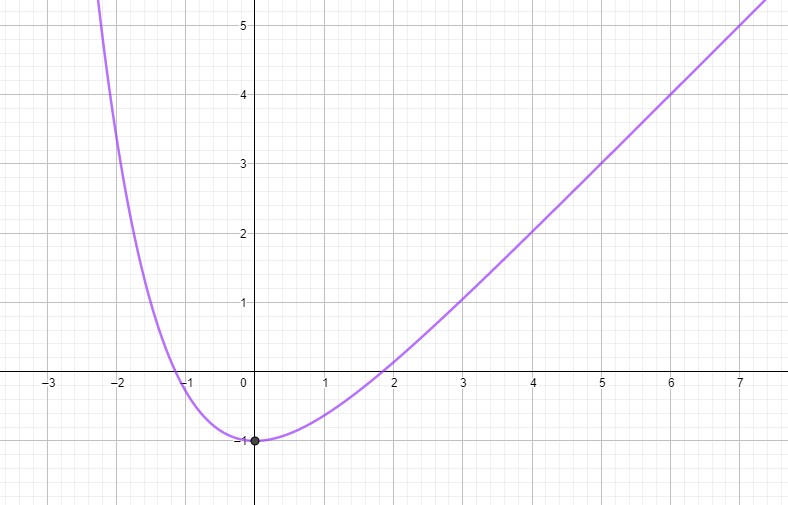
\(f(x)=x-2+e^{-x}\\ f'(x)=1-e^{-x}\\ 1-e^{-x}=0\\ 1=e^{-x}\\ e^0=e^{-x}\Rightarrow x = 0\\ f''(x)=e^{-x}\\ f''(0)=1>0\Rightarrow \text{Tiefpunkt}\)
Die Ableitungen bei b) sind
\(f(x)=x^2\cdot e^x+1\\ f'(x)=e^x\cdot (x^2+2x)\\ f''(x)=e^x\cdot (x^2+4x+2)\)
Gruß, Silvia