Beweise die Gleichung ( Geometrische Reihe?)

Question

Hallo, ich sitze vor folgender Aufgabe:

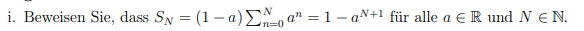
Text erkannt:

i. Beweisen Sie, dass \( S_{N}=(1-a) \sum \limits_{n=0}^{N} a^{n}=1-a^{N+1} \) für alle \( a \in \mathbb{R} \) und \( N \in \mathbb{N} \).

Das die Summe mit a^n die quadratische Reihe , jedoch nicht bis ins unendliche ist, habe ich erkannt. Jedoch scheint es mir unmöglich zu sein diese Gleichung zu beweisen. Muss ich etwas umformen oder eine Definition anwenden, ich bin seit Stunden ratlos.
LG dorfschmied

Answer 1

(1 - a) * ∑ (n = 0 bis N) (a^n)

= ∑ (n = 0 bis N) (a^n) - a * ∑ (n = 0 bis N) (a^n)

= ∑ (n = 0 bis N) (a^n) - ∑ (n = 0 bis N) (a^(n + 1))

= ∑ (n = 0 bis N) (a^n) - ∑ (n = 1 bis N + 1) (a^n)

= (a^0) - (a^(N + 1)) = 1 - a^(N + 1)

Answer 2

Für \(  \sum \limits_{n=0}^{N} a^{n} \) gibt es eine sehr klare Formel.

https://studyflix.de/mathematik/geometrische-summenformel-2407

Das Ergebnis dieser Formel musst du noch mit (1-a) multiplizieren.