Aufgabe:
Auszug aus der Mathe Abschlussprüfung 2013 Nachtermin Bayern.
Aufgabe A 1
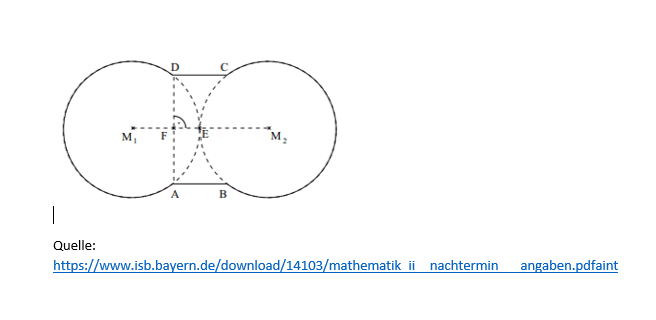
Die nebenstehende Skizze zeigt die Figur, die zum Einbau einer Küchenspüle aus einer Arbeitsplatte ausgesägt werden muss. Die Figur wird begrenzt durch die Kreisbögen BC und DA sowie die parallelen Strecken [AB] und [DC]. Die Kreise \( k_{1}\left(M_{1} ; r=\overline{M_{1} \mathrm{~A}}\right) \) und \( \mathrm{k}_{2}\left(\mathrm{M}_{2} ; \mathrm{r}=\overline{\mathrm{M}_{2} \mathrm{~B}}\right) \) berühren sich im Punkt \( E \in\left[M_{1} M_{2}\right] \)
Es gilt: \( \overline{\mathrm{M}_{1} \mathrm{~A}}=\overline{\mathrm{M}_{2} \mathrm{~B}}=25 \mathrm{~cm} ; \overline{\mathrm{AB}}=\overline{\mathrm{CD}}=20 \mathrm{~cm} \).
Berechnen Sie den Flächeninhalt der ausgesägten Figur.
[Teilergebnis: \( \angle \mathrm{AM}_{1} \mathrm{~F}=53,13^{\circ} \) ]
Quelle: https://www.isb.bayern.de/download/14103/mathematik ii nachtermin angaben.pdif
Problem/Ansatz:
Einerseits hätte die Aufgabe so verstanden, dass die ausgesägte Figur das von mir rot Markierte darstellt. Dabei wurde hier verlangt, dass die gesamte Skizze die Figur ist und dementsprechend die gesamte Skizze berechnet wird. Das verwirrt mich allerdings etwas, da es doch heißt, dass die Figur durch die beiden Kreisbögen und die beiden Strecken begrenzt wird. Andererseits lässt der erste Satz lässt vermuten, dass es sich bei der Figur um die gesamte Skizze handelt, allerdings verstehe ich den Teil mit der Begrenzung nicht.
Wo liegt der (Denk-)Fehler?