Höhe einer Kugelhaube bestimmen

Question

Aufgabe: Höhe einer Kugelhaube bestimmen

Problem/Ansatz:

Mit Hilfe des Artikels "Kugelsegment" in der Wikipedia versuche ich, die Höhe h eines solchen Segments oder der Kugelhaube zu finden.

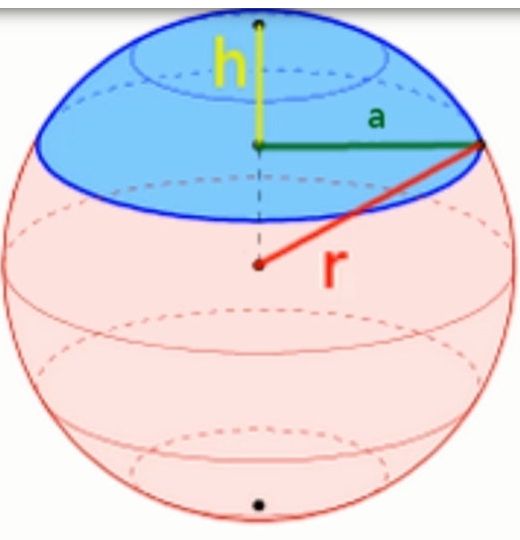
Aus der Zeichnung in der Wikipedia geht hervor, dass nach Pythagoras folgendes gilt:

(1) r^2 = (r – h)^2 + a^2, was sich zu (2) 2rh = a^2 + h^2 umschreiben lässt.

Nun folgt (3) h = r ± √(r^2 – a^2) mit dem Zusatz, dass bei ± das Minus zu wählen ist, wenn das Kugelsegment kleiner als die halbe Kugel groß ist.

Meine Frage: Mit welchen Rechenschritten kommt man von (1) oder (2) nach (3)?
…

Answer 1

(1) auf (2):

Binomische Formel

2rh addieren

r² subtrahieren

(2) auf (3):

2rh subtrahieren

pq-Formel anwenden: \(h_{1,2}= ...\).

Answer 2

Hallo,

wenn du den gestrichelt dargestellten Teil unter h als x bezeichnest, geht die Herleitung sogar ohne "pq-Formel".

r=x+h → h=r-x   im dargestellten Fall.

x²+a²=r² → x=√(r²-a²)

Also h=r-√(r²-a²)

:-)

Answer 3

Hallo,

\(r^2=(r-h)^2+a^2\)

Klammer auflösen:

\(r^2=r^2-2rh+h^2+a^2\quad |-r^2;+2rh\\ 2rh=h^2+a^2\)

Das ist dann (2). Auf beiden Seiten -2rh

\(h^2-2rh+a^2=0\)

pq-Formel anwenden:

\(h_{1,2}=r\pm\sqrt{r^2-a^2}\)

Das ist (3).

Gruß, Silvia