Beweis Sie mit vollständiger Induktion Für alle n ∈ N0 gilt Summe k=0 bis n (k^3) = (Summe k=0 bis n (k))

Question

Aufgabe:

Beweisen Sie per Induktion: Für alle n ∈ N0 gilt Summe k=0 bis n (k^3) = (Summe k=0 bis n (k))

Problem/Ansatz:

Hallo,

ich habe Probleme die obenstehendes Aufgabe zu lösen:

Mein Lösungsansatz ist folgender:

Ich habe bereits Teilschritte gemacht und ganz unten steht bereits was ich zu zeigen habe. Leider komme ich bei den Zwischenschritten nicht weiter.

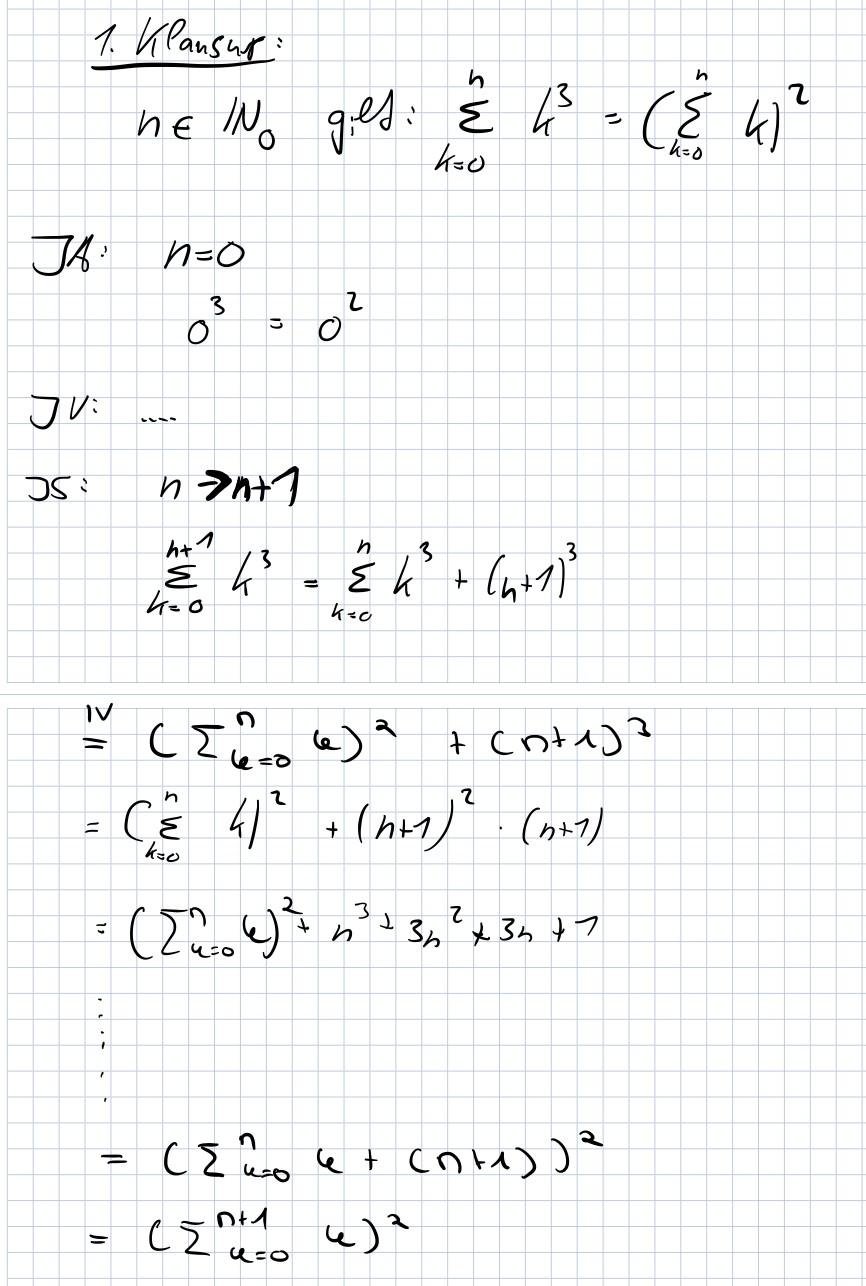
Text erkannt:

1. KPansur:
\( n \in \mathbb{N}_{0} \) gefs: \( \sum \limits_{k=0}^{n} k^{3}=\left(\sum \limits_{k=0}^{n} k\right)^{2} \)
If: \( n=0 \) \( 0^{3}=0^{2} \)
JV: ....
\( \begin{array}{ll}J 5: & n \rightarrow n+1 \\ & \sum \limits_{n=0}^{n+1} k^{3}=\sum \limits_{k=0}^{n} k^{3}+(n+1)^{3}\end{array} \)
\( \stackrel{I V}{=}\left(\sum \limits_{k=0}^{n}(e)^{2}+(n+1)^{3}\right. \)
\( =\left(\sum \limits_{k=0}^{n} 4\right)^{2}+(n+1)^{2} \cdot(n+1) \)
\( =\left(\sum \limits_{n=0}^{n} 6\right)^{2}+n^{3}+3 n^{2}+3 n+1 \)
\( \begin{array}{l} =\left(\sum \limits_{u=0}^{n} u+(n+1)\right)^{2} \\ =\left(\sum \limits_{u=0}^{n+1} u\right)^{2} \end{array} \)

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Die Gauß-Summe sollte aus der Vorlesung oder aus den Übungen bekannt sein:$$\sum\limits_{k=0}^nk=\frac{n(n+1)}{2}$$Die zu zeigende Behauptung lautet also:$$\sum\limits_{k=0}^nk^3=\frac{n^2(n+1)^2}{4}$$

Verannkerung bei \(n=0\):$$\sum\limits_{k=0}^nk^3=\sum\limits_{k=0}^0k^3=0\quad;\quad\frac{n^2(n+1)^2}{4}=\frac{0^2\cdot(0+1)^2}{4}=0\quad\checkmark$$Offensichtlich ist für \(n=0\) die Behauptung erfüllt.

Induktionsschritt von \(n\) auf \((n+1)\):$$\sum\limits_{k=0}^{n+1}k^3=(n+1)^3+\sum\limits_{k=0}^{n}k^3\stackrel{(\text{Ind.Vor.})}{=}(n+1)^3+\frac{n^2(n+1)^2}{4}$$$$\phantom{\sum\limits_{k=0}^{n+1}k^3}=\frac{4(n+1)\pink{(n+1)^2}}{4}+\frac{n^2\pink{(n+1)^2}}{4}=\frac{4(n+1)\pink{(n+1)^2}+n^2\pink{(n+1)^2}}{4}$$$$\phantom{\sum\limits_{k=0}^{n+1}k^3}=\frac{(\;4(n+1)+n^2\;)\cdot\pink{(n+1)^2}}{4}=\frac{(n^2+4n+4)\cdot\pink{(n+1)^2}}{4}$$$$\phantom{\sum\limits_{k=0}^{n+1}k^3}=\frac{(n+2)^2\cdot\pink{(n+1)^2}}{4}=\frac{\pink{(n+1)^2}(n+2)^2}{4}\quad\checkmark$$Damit gilt die Behauptung für alle \(n\in\mathbb N_0\).

Answer 2

Hallo

die Summe über k ist doch bekannt= mit n*(n+1)/2

das musst du wohl verwenden oder mit  ( (∑k) +n+1)^2 vergleichen warum hast du da einfach aufgehört und deine verletze Zeile nicht ausgewertet, d.h. quadriert?

Gruß lul