Hallo,
Wie stelle ich diese gleichung auf?
Die Parameterform einer Gleichung durch 2 Punkte \(A\) und \(B\) ist z.B.$$\vec x = A + t(B-A) = A + t\vec{AB}$$lerne das nicht auswendig, sondern mache Dir selber klar, wieso dieser Term eine Gerade durch 2 Punkte definiert. \(t\) ist dabei der Parameter. Setze mal für \(t\) die Werte \(0\), \(1\), \(2\) oder \(0,5\) ein und schaue, was da raus kommt!
Das bedeutet konkret für die Geraden \(g_1\) und \(g_2\) durch die Punkte \(A\) und \(E\) bzw. \(B\) und \(F\):$$g_1: \quad \vec x = A + r(E-A) =\begin{pmatrix}8\\ 4\\ 3\end{pmatrix} + r\left(\begin{pmatrix}6,5\\ 4\\ 4\end{pmatrix}-\begin{pmatrix}8\\ 4\\ 3\end{pmatrix}\right)= \begin{pmatrix}8\\ 4\\ 3\end{pmatrix} +r\begin{pmatrix}-1,5\\ 0\\ 1\end{pmatrix} \\ g_2: \quad \vec x = B + s(F-B) = \begin{pmatrix}4\\ 8\\ 3\end{pmatrix}+s\left(\begin{pmatrix}4\\ 6,5\\ 4\end{pmatrix}-\begin{pmatrix}4\\ 8\\ 3\end{pmatrix}\right) = \begin{pmatrix}4\\ 8\\ 3\end{pmatrix}+s\begin{pmatrix}0\\ -1,5\\ 1\end{pmatrix}$$um den Schnittpunkt zu berechnen, setzt man die beiden Geraden gleich. Im Falle eines Schnittpunkts müssen sie ja einen Punkte gemeinsam haben!$$\begin{aligned} \begin{pmatrix}8\\ 4\\ 3\end{pmatrix} +r\begin{pmatrix}-1,5\\ 0\\ 1\end{pmatrix} &= \begin{pmatrix}4\\ 8\\ 3\end{pmatrix}+s\begin{pmatrix}0\\ -1,5\\ 1\end{pmatrix} \\ \begin{pmatrix}8\\ 4\\ 3\end{pmatrix} - \begin{pmatrix}4\\ 8\\ 3\end{pmatrix}&= s\begin{pmatrix}0\\ -1,5\\ 1\end{pmatrix} +r\begin{pmatrix}1,5\\ 0\\ -1\end{pmatrix} \\ \begin{pmatrix}4\\ -4\\ 0\end{pmatrix} &= s\begin{pmatrix}0\\ -1,5\\ 1\end{pmatrix} +r\begin{pmatrix}1,5\\ 0\\ -1\end{pmatrix} \end{aligned}$$aus der ersten Gleichung (Zeile) folgt \(r = 8/3\) und aus der zweiten folgt \(s = 8/3\). Setzt man beides in die dritte Zeile ein, so geht diese auf. D.h. der Schnittpunkt \(S\) existiert und liegt bei $$S = g_1\left(r=\frac83\right) = \begin{pmatrix}8\\ 4\\ 3\end{pmatrix} + \frac 83\begin{pmatrix}-1,5\\ 0\\ 1\end{pmatrix} = \begin{pmatrix}4\\ 4\\ 17/3\end{pmatrix}$$und so sieht das im Bild aus
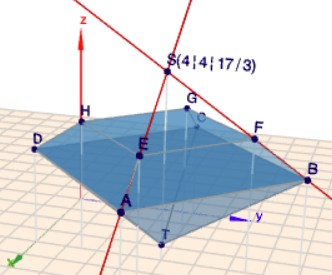
(klick auf das Bild)
zu (b) der Umfang ist die Summe aus den Abständen der drei Punktepaare des Dreiecks. Den Flächeninhalt \(F\) berechnet man über das Kreuzprodukt $$F_{\triangle ABT} = \frac 12 \left|\vec{AB} \times \vec {AT}\right| \quad \vec {AB} = B-A, \space \vec{AT} = T-A$$
zu (c) zum Winkel \(\angle BAT\) kommt man über das Skalarprodukt.$$\cos\left(\angle BAT\right) = \frac{\vec{AB} \cdot \vec{AT}}{|\vec{AB}| \cdot |\vec{AT}|}$$
und falls Du mit (d) nicht klar kommst, so solltest Du Dich nochmal melden.
Gruß Werner