Welchen Wert hat die zweite Ableitung f^{\prime \prime}(x) im Punkt C?

Question

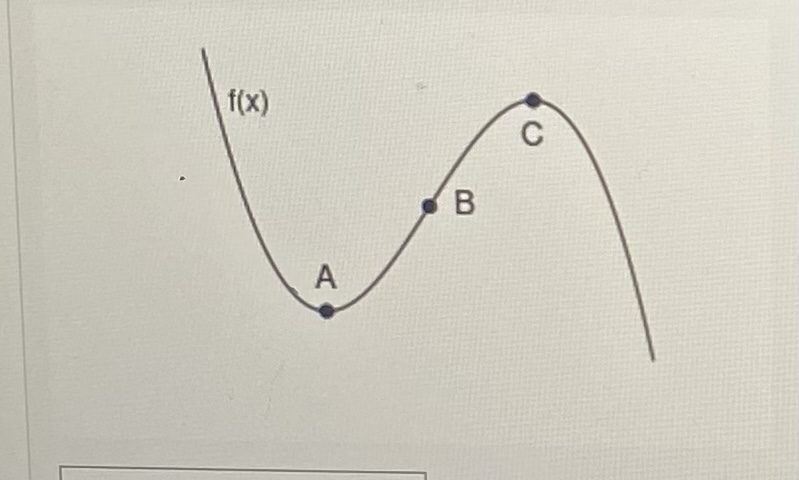
Die folgende Grafik zeigt drei kritische Punkte der Funktion \( f(x) \) bzw. ihrer Ableitung \( f^{\prime}(x) \). Die Funktion ist gegeben durch:
\( f(x)=-0.67 x^{3}+1.24 x^{2}+1.12 x-4.28 \)
Welchen Wert hat die zweite Ableitung \( f^{\prime \prime}(x) \) im Punkt C?

Problem/Ansatz:

Kann mir jemand bitte helfen… ich verstehe nicht genau was nun zu tun ist… und wie die Schritte sind.

Answer 1

Hallo,

C ist der Hochpunkt der Funktion. Seinen x-Wert berechnest du, indem du die 1. Ableitung = 0 setzt und nach x auflöst.

Setze dein Ergebnis dann in die 2. Ableitung ein.

Gruß, Silvia

Answer 2

f(x) = - 0.67·x^3 + 1.24·x^2 + 1.12·x - 4.28

f'(x) = - 2.01·x^2 + 2.48·x + 1.12 = 0 --> x = 1.585315427 (Für die Stelle C)

f''(x) = 2.48 - 4.02·x

f''(1.585315427) = 2.48 - 4.02·1.585315427 = -3.892968016