Wie würde dieser Graph als Funktionsgleichung aussehen?

Question

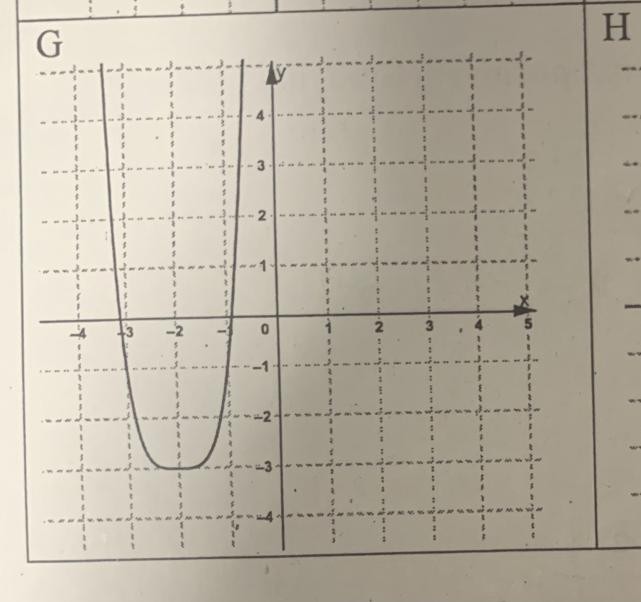
Aufgabe: Wie würde dieser Graph als Funktionsgleichung aussehen?

Problem/Ansatz:

Ich habe ein LGS mit:

f(-2) = -3
f(-1) = -1
f'(-2) = 0

aufgestellt und bekam die Funktionsgleichung: 2x^2+8x+5:

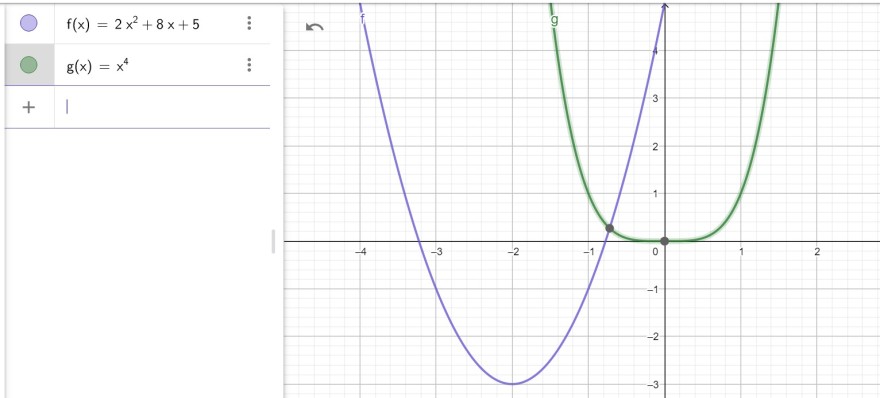
Das ist aber falsch, da die Funktion die Form von x^4 haben muss.

Wie stelle ich dazu am besten ein LGS auf?

ax^4+bx^3+cx^2+dx+e wird nicht funktionieren, da die Funktion nur einen Tiefpunkt hat und damit also auch nicht jeder Koeffizient vorhanden sein muss.
aus ax^4 + cx^2 wird wiederum eine (halb)normale Parabel
ax^4 + e scheint die einzige Lösung zu sein, aber dadurch würde man ja nur die x^4 Funktion nach oben oder unten verschieben.

Wie muss man hier vorgehen?

Comments

Der Exponent 4 sollte noch begründet werden.

Answer 1

f(x) = ax^4+bx^2+ c

x= -1 und x= -3 sind keine x-Werte von f(x).

Schau mal genau hin!

f'(-2) = 0

Comments

f(x) = ax4+bx2+ c

Das ist falsch. Mit dieser falschen Herangehensweise erhalte ich so eine Funktion:

x= -1 und x= -3 sind keine x-Werte von f(x).

Schau mal genau hin!

Lesen bzw. Grundlagen in Mathematik sind bei dir auch mangelhaft.

f(-2) = -3   Bedeutet, dass die Funktion an der Stelle -2, den y-Wert -3 annimmt!
f(-1) = -1   Bedeutet, dass die Funktion an der Stelle -1, den y-Wert -1 annimmt!

Answer 2

Hallo,

\(ax^4\) + e scheint die einzige Lösung zu sein, aber dadurch würde man ja nur die \(x^4\) Funktion nach oben oder unten verschieben.
Wie muss man hier vorgehen?

genauso wie auch bei einer Parabel in der Scheitelpunktform. Im Prinzip müsste das so aussehen$$f(x) = (x-(-2))^2 + 3$$nur hoch 2 reicht hier nicht aber Dein Ansatz mit hoch 4 war schon richtig. Wenn man die Funktion dann noch etwas streckt, dann passt es:

$$f\left(x\right)=2\left(x+2\right)^{4}-3$$Tipp: Man kann jede Funktion um \(\Delta x\) nach rechts verschieben (bei \(\Delta x \lt 0\) dann nach links), wenn man in der Funktion das \(x\) durch \((x-\Delta x)\) ersetzt.$$f(x) \to f(x-\Delta x)$$

Comments

Es ist also UNMÖGLICH,...

diese Funktion in der Normalform darzustellen
diese Funktion mit einem LGS zu berechnen.

Stimmt es?

---

Äh!? Definiere: Normalform einer Funktion (was ist das?)

und mit einem linearen Gleichungssystem (LGS) hat dies nichts zu tun, da  eine Funktion kein Gleichungssystem ist und diese Funktion nicht linear ist.

---

und hoch 4 auch nicht   doch.

---

und hoch 4 auch nicht doch.

Ja - ich war nicht schnell genug mit der Korrektur. Ist erledigt (s.o.)

---

Äh!? Normalform einer Funktion (was ist das?)

Mathe Klasse 7...

Das wäre sicher was für Sie.

und mit einem linearen Gleichungssystem (LGS) hat dies nichts zu tun

Auch das ist falsch, denn mit einem LGS kann man Funktionsgleichungen bestimmen. Sie können anscheinend nur eine ganz kleine (Scheitelpunktform) Gleichung aufschreiben.

---

Zurückgezogen wegen Überschneidung

---

mit einem LGS kann man Funktionsgleichungen bestimmen.

Ja natürlich kann man das, aber danach hast Du ja nicht gefragt! Du fragtest:

Wie würde dieser Graph als Funktionsgleichung aussehen?

Diese Frage habe ich Dir beantwortet ;-)

Der Ansatz mit einer Parabel, d.h. eines Polynom 2. Grades war schlicht nicht ausreichend.

Es ist also UNMÖGLICH,...
diese Funktion in der Normalform darzustellen

Jetzt mal im Ernst, kannst Du wirklich nicht den Term \((x+2)^4-3\) expandieren? Und selbst wenn es Dir nicht auf Anhieb gelingt, so solltest Du doch wissen, dass es möglich ist.

---

Sie können anscheinend nur ...

"Hikoba" ist das neue Wort für "arrogant, unverschämt".

---

Könntest du mir bitte bei meiner neuesten Aufgabe helfen...

Komme da irgendwie nicht weiter(a-c)

Danke :)

---

@Hikoba: Dein Betragen hier im Forum ist nicht was wir als "Höfliches Miteinander" verstehen! Deine verbalen Angriffe sind zu unterlassen! Du bekommst hier Hilfe! Umsonst! Mit viel Mühe gemacht! Sei Dir dabei bewusst, dass wir nichts über Dich wissen und einen Wissensstand nur abschätzen können. Wenn Dir die Hilfe nicht zusagt steht es Dir frei Dich anderweitig nach Unterstützung umzuschauen.

Answer 3

Scheitelpunktform einer Parabel 4. Grades

f(x) = 2·(x + 2)^4 - 3

Ausmultipliziert ergibt das die allgemeine Form

f(x) = 2·x^4 + 16·x^3 + 48·x^2 + 64·x + 29

Diese Darstellung würde man aber eigentlich nicht mit gutem Gewissen empfehlen.

Natürlich könnte man es auch über ein LGS herleiten. Verwende dazu http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle.

Eigenschaften

f(-3) = -1
f(-1) = -1
f(-2) = -3
f'(-2) = 0
f''(-2) = 0

Gleichungssystem

81a - 27b + 9c - 3d + e = -1
a - b + c - d + e = -1
16a - 8b + 4c - 2d + e = -3
-32a + 12b - 4c + d = 0
48a - 12b + 2c = 0

Errechnete Funktion und Ableitung(en)

f(x) = 2·x^4 + 16·x^3 + 48·x^2 + 64·x + 29
f'(x) = 8·x^3 + 48·x^2 + 96·x + 64
f''(x) = 24·x² + 96·x + 96
f'''(x) = 48·x + 96
f''''(x) = 48