2)Gegeben sind lineare Gleichungen mit 2 Variablen. Gleichung
(1): 2x + 4y = 4 und gleichung
(2): 6x - 2y = 12
a)Gib je zwei Zahlenpaare an,die Lösungen der Gleichung(1) bzw. der Gleichung (2) sind
Lösung für Gleichung (1) Zahlenpaare: (0 | 1) (2 | 0)
Lösung für Gleichung (2) Zahlenpaare: (0 | -6) (2 | 0)
b) Ergänze die Zahlenpaare(2/3;...) und (...;-9) so,dass sie Lösungen der Gleichung (1) sind.
2x + 4y = 4
4y = 4 - 2x
y = 1 - 0,5 x = 1 - 0,5 * 2/3 = 2/3 => (2/3; 2/3)
2x + 4y = 4
2x = 4 - 4y
x = 2 - 2y = 2 - 2*(-9) = 20 => (20; -9)
c) Stelle beide Gleichungen nach y um,sodass Gleichungen der Form y=mx+n entstehen.
y = -0,5x + 1 [Hab ich schon aus der vorherigen Aufgabe]
6x - 2y = 12
-2y = -6x + 12
y = 3x - 6
d) Überprüfe grafisch deine Ergebnisse zu den Aufgaben 4 a u. b
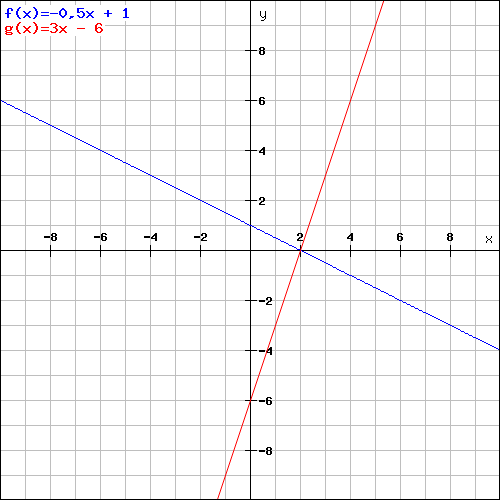
e) Löse das durch die beiden Gleichungen gebildete lineare Gleichungssystem rechnerisch
-0,5x + 1 = 3x - 6
-3,5x = -7
x = 2
y = 3*2 - 6 = 0
Rechnerische Lösung bei (2 | 0)
f) Lies die Koordinaten des Schnittpunktes S beider Graphen ab und vergleiche dein Ergebnis mit dem der Aufgabe e)
Der Schnittpunkt stimmt mit dem rechnerischen Ergebnis überein.
g)Unter welchen Winkeln schneiden die Graphen der Funktion zu den Gleichungen (1) und (2) die x-Achse?
y1 = -0,5x + 1
y2 = 3x - 6
α1 = arctan(-0,5) = -26,57°
α2 = arctan(3) = 71,57°