Aufgabe mit Lösung:
2. Beweisen Sie: In einem beliebigen Parallelogramm halbieren die Diagonalen einander.
LÖSUNG:
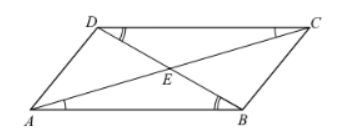
- Sei \( A B C D \) ein Parallelogramm, \( E \) der Schnittpunkt der Diagonalen.
- \( \angle(A B E) \equiv \angle(C D E) \) nach Wechselwinkelsatz
- \( \angle(B A E) \equiv \angle(D C E) \) nach Wechselwinkelsatz
- \( |A B|=|C D| \quad \) da nach einem bekannten Satz gegenüberliegende Seiten im Parallelogramm gleich lang sind
- \( \Rightarrow \Delta A B E \equiv \Delta C D E \quad \) nach dem Kongruenzsatz ,wsw"
- \( \Rightarrow|B E|=|D E| \) und \( |A E|=|C E| \), was zu beweisen war.
WSW besagt: Wenn zwei Dreiecke in einer Seite und zwei gleichliegenden Winkeln übereinstimmen, dann sind sie kongruent.
Aber was bitte sagt die Lösung darüber aus, dass die Diagonalen sich einander halbieren?