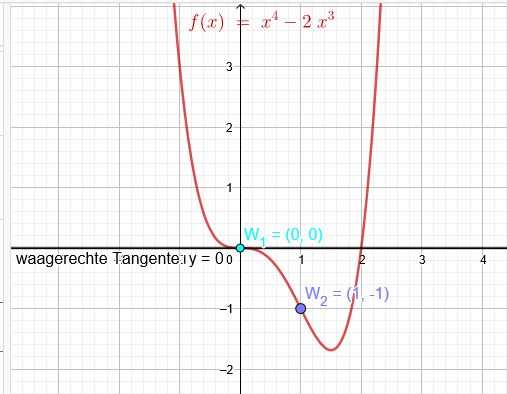
Der Graph \( G_{f} \) einer in \( \mathbb{R} \) definierten Funktion \( f: x \mapsto a x^{4}+b x^{3} \) mit \( a, b \in \mathbb{R} \) besitzt im Punkt \( \mathrm{O}(0 \mid 0) \) einen Wendepunkt mit waagrechter Tangente. \( W(1 \mid-1) \) ist ein weiterer Wendepunkt von \( G_{f} \). Bestimmen Sie mithilfe dieser Information die Werte von a und b.
1.) In \( \mathrm{O}(0 \mid 0) \) ein Wendepunkt mit waagerechter Tangente:
Hier ist eine 3-fache Nullstelle:
\(f(x)=a\cdot x^3(x-N)\)
2.) \( W(1 \mid-1) \) ist ein weiterer Wendepunkt
\(f(1)=a\cdot (1-N)\)
\(a\cdot (1-N)=-1\) → \(a=\frac{1}{N-1}\)
\(f(x)=\frac{1}{N-1}\cdot [x^4-Nx^3]\)
3.) Wendepunkteigenschaft
\(f'(x)=\frac{1}{N-1}\cdot [4x^3-3Nx^2]\)
\(f''(x)=\frac{1}{N-1}\cdot [12x^2-6Nx]\)
\(f''(1)=\frac{1}{N-1}\cdot [12-6N]\)
\(\frac{1}{N-1}\cdot [12-6N]=0\) → \(N=2\) \(a=\frac{1}{2-1}=1\)
\(f(x)=x^3(x-2)=x^4-2x^3\)
\(a=1\) \(b=-2\)
\(f(x)=x^3(x-2)=x^4-2x^3\)