Extremwertproblem Rechteck Parabel

Question

Text erkannt:

auf der Parabel mit der Gleichs liegen auf den Koordinatenachsen, ein Eckpunkt a) Wie lang müssen die Seitenlä \( y=-0,25 x^{2}+4 \). inhalt maximal wird?
b) Wie lang müssen die Seitenlängen des Rechtecks sein, damit sein Umfang maximal wird?

Comments

Du solltest Deine Fragen schon in einer lesbaren Form einstellen.

Answer 1

U= 2*(x+ f(x)) = Umfang des halben Rechtecks

U(x) = 2*(x-0,25x^2+4= = -0,5x^2+2x+4

U'(x)=0

-x^2+2x = 0

-x(x-2) = 0

x = 0 v x=2

-> x= 2 -> l=2*2== 4

y= 3 = b

Answer 2

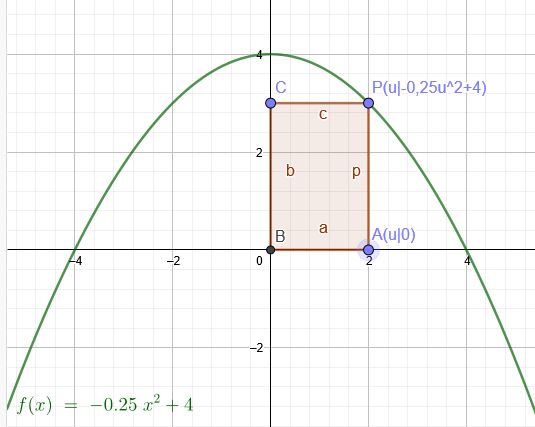
a) \(A(u)=u*(-0,25u^2+4)=-0,25u^3+4u\) soll maximal werden.

 \(A´(u)=-0,75u^2+4\)

                 \(-0,75u^2+4=0\)

                      \(-\frac{3}{4}u^2+4=0\)

                            \(u^2=\frac{16}{3}\)

                               \(u=\frac{4}{3}*\sqrt{3}\)

\(f(\frac{4}{3}*\sqrt{3})=-\frac{1}{4}*\frac{16}{3}+4=\frac{8}{3}\)

Versuche jetzt mal den Weg zum maximalen Umfang.