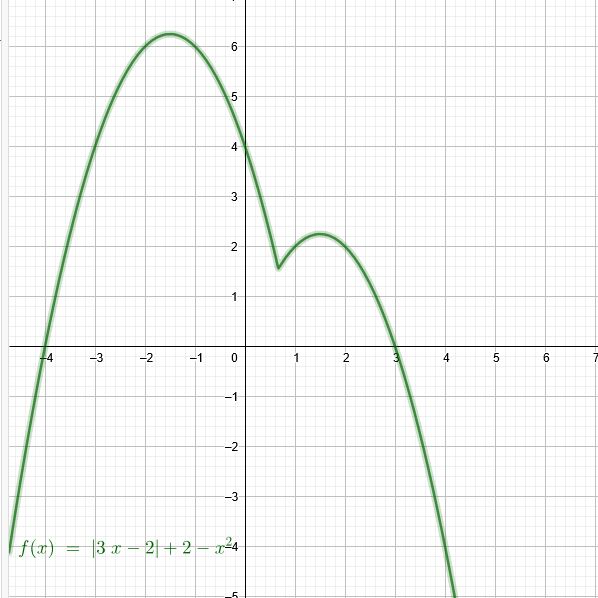
\( |3 x-2|+2=x^{2} \)
\( |3 x-2|=x^{2}-2|^{2} \)
\( (3 x-2)^2=(x^{2}-2)^{2} \)
\( (3 x-2)^2-(x^{2}-2)^{2}=0 \)
\( [(3 x-2)+(x^{2}-2)]*[(3 x-2)-(x^{2}-2)]=0 \)
1.)\((3 x-2)+(x^{2}-2)=0\)
\(x₁=-4∨x₂=1\)
2.)\( (3 x-2)-(x^{2}-2)=0\)
\(x₃=0∨x₄=3\)
Probe, weil Quadrieren keine Äquivalenzumformung ist:
\( |3 *(-4)-2|+2=(-4)^{2} \) \( |-12-2|+2=16 \) \( 14+2=16 \) ✓
\( |3 *1-2|+2=(1)^{2} \) ist falsch
\( |3 *(0)-2|+2=(0)^{2} \) ist falsch
\( |3 *3-2|+2=3^{2} \)✓
Lösungen somit \(-4 ∨ 3\)