Aufgabe:
Wie kann man mithilfe einer Determinante eine eindeutige Lösung diesen Randwertproblemen zeigen/beweisen?
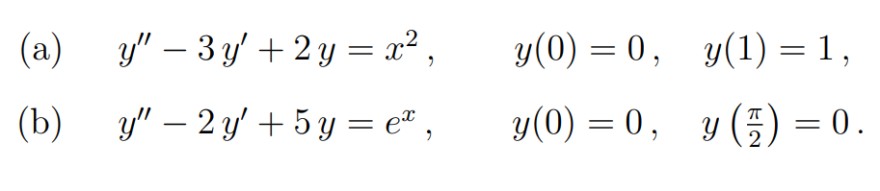
Text erkannt:
(a) \( \quad y^{\prime \prime}-3 y^{\prime}+2 y=x^{2}, \quad y(0)=0, \quad y(1)=1 \),
(b) \( \quad y^{\prime \prime}-2 y^{\prime}+5 y=e^{x}, \quad y(0)=0, \quad y\left(\frac{\pi}{2}\right)=0 \).
Problem/Ansatz:
Also ich habe von beiden die homogene Lösung ausgerechnet.
a) C1cos(\( \frac{3}{2} \)+\( \sqrt{\frac{1}{2}} \)*x)+ C2sin(\( \frac{3}{2} \)-\( \sqrt{\frac{1}{2}} \)*x)
b)C1cos(1+2*x) + C2sin(1-2*x)
aber ich weiß nicht mehr weiter kann mir jemand weiter helfen?