f(x) = x^2 - 2·x - 15·LN(x^2 + 9) + 6·ARCTAN(1/3·x)
f'(x) = 2·x·(x + 2)·(x - 3)/(x^2 + 9)
f''(x) = 2·(x^4 + 33·x^2 - 18·x - 54)/(x^2 + 9)^2
a) Geben Sie die Definitionsbereich von f an (Begründung!).
D = R
Der Ausdruck im LN ist immer positiv und der ARCTAN hat keine Einschränkung im Definitionsbereich.
b) Bestimmen Sie alle Bereiche, auf denen f monoton ist und geben Sie an, ob f dort monoton steigend oder fallend ist. Bestimmen Sie alle relativen Minima un Maxima (falls etwas davon nicht existiert, muss das erwähnt und begründet werden). Hinweis: ableiten, zusammenfassen!
Extremstellen f'(x) = 0
2·x·(x + 2)·(x - 3) = 0
x = 0 oder x = -2 oder x = 3
f''(-2) > 0 --> Tiefpunkt
f''(0) < 0 --> Hochpunkt
f''(3) > 0 --> Tiefpunkt
Anstatt über die 2. Ableitung zu gehen hätte man auch die Steigung vor und nach den Stellen ausrechnen können.
Jetzt kannst du aus den Infos auch die Monotonie angeben
c) Was können Sie aus den Ergebnissen aus a) und b) hinsichtlich der Existenz und Lage absoluter Extrema sagen?
Das dürfte jetzt auch klar sein.
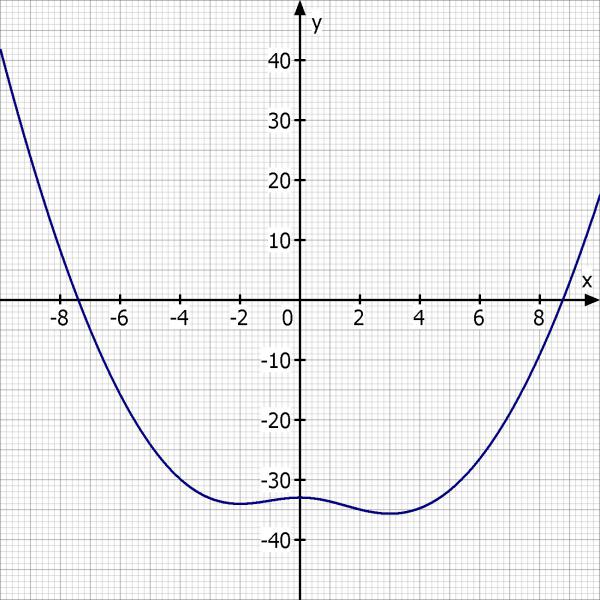
Ich füge noch eine Skizze an: