Zeige, dass die Funktionenschar nur eine Nullstelle besitzt

Question

Aufgabe:

Funktionenschar \( f_{t}(x)=4 x^{2}-4 \cdot t \cdot x+t^{2}, x \in \mathbb{R}, t \in \mathbb{R} \)
1) Zeige, dass der Graph von \( f(t) \) genau eine Nullstelle besitzt
2) Bestimme \( t \) so, dass gilt \( \int \limits_{0}^{t} f_{t}(t) d x=9 \)

Nullstelle einer Funktionenschar zeigen

Und danach t bestimmen, sodass das Integral von 0-t=9 ergibt

Siehe Bild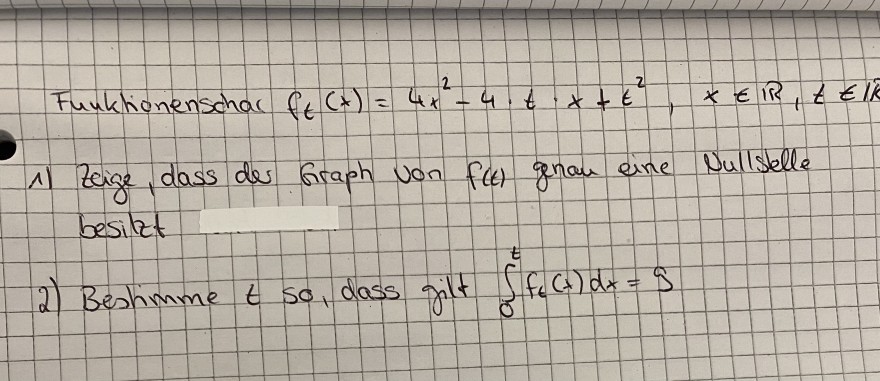

Problem/Ansatz:

Ich muss ft(x)= 0 setzen oder nicht?

Komme aber absolut nicht weiter.

Comments

Das ist die Funktion bei Veränderung des Parameters t:

Answer 1

\( 4 x^{2}-4 \cdot t \cdot x+t^{2} = 0\) <=>  \( (2x-t)^{2} = 0\) <=> 2x=t <=> x = t/2

Also genau eine Nullstelle.

\( \int\limits_0^t( 4 x^{2}-4 \cdot t \cdot x+t^{2}) dx = 9 \)

\( [\frac{4}{3} x^{3}-2 \cdot t \cdot x^2+xt^{2}]_0^t= 9 \)

\( (\frac{4}{3} t^{3}-2 \cdot t \cdot t^2+t\cdot t^{2}) - 0= 9 \)

\( \frac{4}{3} t^{3}-2t^3+t^{3}= 9 \)

\( \frac{1}{3} t^{3}= 9 \)    <=>  t^3 = 27   <=>   t=3

Comments

Vielen Dank, auch wenn ich die Integralrechnung noch nicht verstehe.

---

Das Integral berechnet den Flächeninhalt unter der Funktion \( f_{t}(x) \) zwischen den Grenzen 0 und t.

Um dies zu berechnen, wird die Integralfunktion \( F(x)=\int f_{t}(x) d x \) bestimmt und die Werte von \( F(0) \) und \( F(t) \) berechnet. Der Unterschied zwischen diesen beiden Werten entspricht der gesuchten Fläche.

In diesem Fall wird die Integralfunktion von der Funktion \( f_{t}(x) \) berechnet und die Integralrechnung wird ausgeführt, um das Integral von 0 bis \( t \) zu berechnen. Der Ausdruck \( \left[\frac{4}{3} x^{3}-2 \cdot t \cdot x^{2}+x t^{2}\right]_{0}^{t} \) bezieht sich darauf, dass der Wert des Integrals bei \( x=0 \) und \( x=t \) berechnet wird.

So ergibt sich die Gleichung \( \left(\frac{4}{3} t^{3}-2 \cdot t \cdot t^{2}+\right. \) \( \left.t \cdot t^{2}\right)-0=9 \) mit der Lösung \( \mathrm{t}=3 \)

---

Ahja ich muss ja erst aufleiten. Hatte mich nämlich grad gefragt wieso hoch 3

Answer 2

Hallo,

ja, das ist richtig. Wende die pq-Formel an:

\(4x^2-4tx+t^2=0\\ x^2-tx+\frac{1}{4}t^2=0\\ x_{1,2}=0,5t\pm \sqrt{0,25t^2-0,25t^2}\\ x=0,5t\)

Gruß, Silvia

Comments

Danke, auf die Formel hätte ich auch selbst kommen können

---

Es gab Zeiten (vor Einführung digitaler Werkzeuge), da erkannten Schüler*innen binomische Formeln [wie 4x²-4xt+t²=(2x-t)²] 100 m gegen den Wind.