Nun zu meiner Frage: Wie erhalte ich den Parameterwert mit dem die beiden Funktionen nur einen Schnittpunkt besitzen?

Question

Aufgabe:

Hallo,
wenn man die Schnittpunkte zwischen einer Funktionsschar (lineare Funktion) und einer quadratischen, nach oben geöffneten und nach rechts verschobenen Funktion berechnen will, stellt man ja zu erst gleich und löst dann später mit PQ-Formel, ABC Formel oder quadratischer Ergänzung auf und erhält x1 und x2 als Schnittpunkte. Bei einer Funktionsschar dessen veränderlicher Parameter sich auf die Verschiebung auf der Y-Achse bezieht, erhält man ja grundsätzlich unendliche viele Schnittpunkte.

Nun zu meiner Frage: Wie erhalte ich den Parameterwert mit dem die beiden Funktionen nur einen Schnittpunkt besitzen? Also wenn die lineare Funktion die quadratische Funktion unten am Scheitelpunkt nur ein Mal berührt.

Answer 1

\(f(x)=\frac{1}{3}x^2+2x+1 \)      \(g(x)=3x+3+k\)

\(\frac{1}{3}x^2+2x+1=3x+3+k \)     

\(\frac{1}{3}x^2-x=2+k \)   

\(x^2-3x=6+3k \) 

\((x-\frac{3}{2})^2=6+3k+(\frac{3}{2})^2=3k+\frac{33}{4} \)

Berührpunkt:

\(B(\frac{3}{2}| \frac{1}{3}*(\frac{3}{2})^2+2*\frac{3}{2}+1)  \)  → \(B(\frac{3}{2}|\frac{19}{4}) \)

\(g(\frac{3}{2})=3*(\frac{3}{2})+3+k=\frac{19}{4}\)  →  \(k=-\frac{11}{4}\)

Comments

Vorab danke für deinen Lösungsweg :) Ich habe eine Frage dazu:

Woher weiß du, dass bei dem Berührungspunkt B der X Wert 3/2 ist?

Stehe gerade aufm Schlauch :,)

---

Ist es, weil 3/2 ein Punkt sein muss?

---

Ich habe mal eine erklärende Zeichnung angefertigt:

---

Hab ich mir auch schon über GeoGebra angeschaut, aber woher kam dir der Gedanke beim Rechnen, dass du die 2/3 nutzt?

---

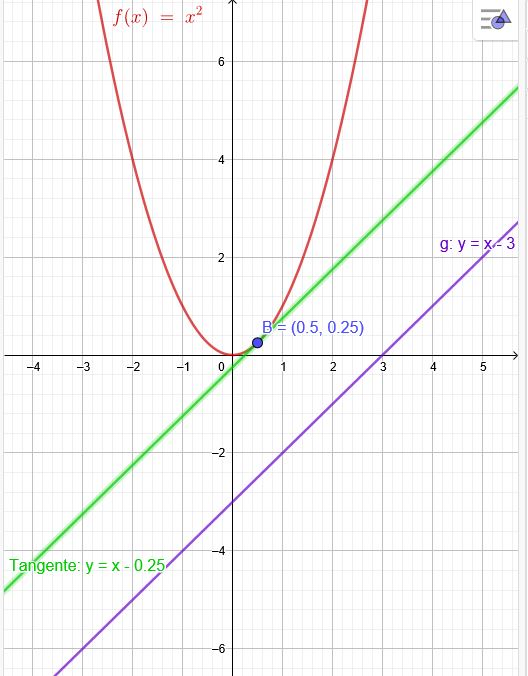
Ich nehme mal \(f(x)=x^2\) und  \(g: y=x-3\)

Ich setze nun  \(f(x)=g\):

\(x^2=x-3\)

\(x^2-1x=-3\)

\((x-0,5)^2=-3+0,25=-2,75=2,75i^2|\sqrt{~~}\)

1.) \(x-0,5=\sqrt{2,75i^2}=i*\sqrt{2,75}\)

\(x₁=0,5+i*\sqrt{2,75}\)

2.) \(x-0,5=-i*\sqrt{2,75}\)

\(x₂=0,5-i*\sqrt{2,75}\)

Der Berührpunkt der Parallelen zu \(g: y=x-3\) ist nun \(B(0,5|0,25)\)

Diesen Sachverhalt habe ich zur Lösung deiner Aufgabe benutzt.

---

Hab ich mir auch schon über GeoGebra angeschaut, aber woher kam dir der Gedanke beim Rechnen, dass du die 2/3 nutzt?

Das steht in meiner Lösung schon seit geraumer Zeit

x = 3/2

mfg Georg

Answer 2

wenn man die Schnittpunkte zwischen einer Funktionsschar (lineare Funktion) und einer quadratischen, nach oben geöffneten und nach rechts verschobenen Funktion berechnen will, stellt man ja zu erst gleich

Ja.

und löst dann später mit PQ-Formel, ABC Formel oder quadratischer Ergänzung auf

Ja, weil das Gleichsetzen eine quadratische Gleichung liefert.

Bei einer Funktionsschar dessen veränderlicher Parameter sich auf die Verschiebung auf der Y-Achse bezieht, erhält man ja grundsätzlich unendliche viele Schnittpunkte.

So würde ich das nicht auffassen. Stattdessen erhältst du einen Term als \(x_1\) und einen Term als \(x_2\). In diesen Termen kommt der Parameter vor.

Wie erhalte ich den Parameterwert mit dem die beiden Funktionen nur einen Schnittpunkt besitzen?

Die Terme für \(x_1\) und \(x_2\) gleichsetzen und die Gleichung lösen.

Comments

Das heißt, wenn ich mit der PQ-Formel gearbeitet habe, steht ja unter der Wurzel der Parameter (z.B. k) von der Funktionsschar. Und dann? Muss man dann die PQ Formel mit + und - gleichsetzen?

---

Ich hab hier auch ein Beispiel:

f(x) = 1/3x² + 2x +1

g_k(x) = 3x + 3 + k

k ist besagter Parameter

---

Beispiel.

\(\begin{aligned}f(x) &= \frac{1}{3}x^2 + 2x + 1\\g_k(x) &= 3x + 3 + k\\\\\frac{1}{3}x^2 + 2x + 1 &= 3x+3+k\\\\x_1 &= \frac{3}{2} - \sqrt{3k+\frac{33}{4}}\\x_2 &= \frac{3}{2} + \sqrt{3k+\frac{33}{4}}\\\\x_1 &= x_2\\\frac{3}{2} - \sqrt{3k+\frac{33}{4}}&=\frac{3}{2} + \sqrt{3k+\frac{33}{4}}\end{aligned}\)

Answer 3

Beim Gleichsetzen entsteht doch eine Wurzel mit ± davor. Wenn der Term unter der Wurzel (der noch den Parameter enthält) gleich Null ist, dann gibt es nur eine Lösung.

Answer 4

Hallo,

Also wenn die lineare Funktion die quadratische Funktion unten am Scheitelpunkt nur ein Mal berührt.

Wenn eine Gerade eine Parabel nur im Scheitelpunkt berühren soll, ist es eine Parallele zur x-Achse der Form y = a, mit a y-Koordinate des Scheitelpunkts.

Gruß, Silvia

Answer 5

Bei Verwendung der pq-Formel:

Setze die Diskriminante \(p^2-4q=0\) und bestimme daraus

den gesuchten Parameter.

Answer 6

f = a * x^2 + b * + c
g = m * x + b

Es soll nur 1 Schnittpunkt geben = Berührpunkt
Die Steigung der beiden Funktionen ist gleich.

f ´ ( x ) = g ´ ( x )
und
der Funktoinswert ist gleich
f ( x ) = g ( x )

Sonst gib einmal ein Beispiel
f ( x ) =
g ( x ) =

Comments

f(x) = 1/3x² + 2x + 1

g_k(x) = 3x + 3 + k

---

f (x) = 1/3*x^2 + 2x + 1
g (x) = 3x + 3 + k

f = g
1/3*x^2 + 2x + 1 = 3x + 3 + k

f´( x ) = 2/3 * x + 2
g ´( x ) = 3

f ´= g ´
2/3 * x + 2 = 3
2/3 * x + 2 = 3
2/3 * x = 3 - 2
x = 3/2

1/3*x^2 + 2x + 1 = 3x + 3 + k
1/3 * (3/2)^2 + 2 * 3/2 + 1 = 3 * 3/2 + 3 + k

k = -11/4
g (x) = 3x + 3 + k
g (x )= 3*x + 1/4