Aufgabe:
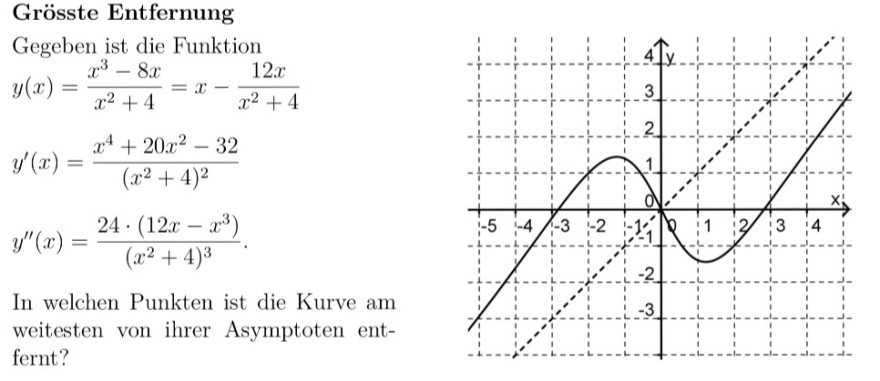
Gegeben ist die Funktion y(x) = \( \frac{x^{3}-8x}{x^{2}+4} \) = x - \( \frac{12x}{x^{2}+4} \)
In welchen Punkten ist die Kurve am weitesten von ihrer Asymptoten (a(x) = x) entfernt?
Problem/Ansatz:
Ich komme bei dieser Aufgabe nicht weiter. Mein erster Ansatz wäre gewesen, die Asymptote a(x) = 1 mit der Funktion y(x) gleichzusetzten, abzuleiten und davon ein Maximum zu bilden, aber ich glaube nicht das es so klappt.
Vielen Dank für jede Hilfe