Aufgabe:
Wie kann man aus 3 kongurenten Quadraten ein neues grösseres machen ohne die anderen zu schneiden? Nur Falten ist erlaubt.
Problem/Ansatz:
Wie geht das?
Text erkannt:
Sie haben drei kongruente quadrate. Legen sie die quadrate nebeneinander oder stapeln sie sie so, dass die drei quadrate ein grösseres quadrat als das original bilden. Sie können die quadrate falten, aber sie können sie nicht schneiden oder reissen.
Hallo
wie liegen die denn zueinander? und was sind die anderen Bedingungen ausser größer?
Die 3 kongurenten Quadrate müssen zusammen ein grösseres geben als sie schon sind. Aber es steht nicht wie gross sie sein müssen.
z. B. können sie 5 cm auf 5 cm sein und alle 3 zusammen müssen dann zu einem grösserem Quadrat werden als 5 x 5 cm. Dabei darf nur gefaltet werden. und nicht geschnitten
Hallo nochmal: sind die 3 einzeln und du sollst die gefalteten aneinander legen?
lul
Ja es sind 3 einzelne Stücke, die frei gelegen werden können
Verstehen tu ich das Monty Konstrukt allerdings net - also geb auch mal meinen Senft dazu:
hin geruckelt etwa
War das so gedacht?
Sehr schöne Lösung. Die Fläche des größeren Quadrats ist \(\Phi\) mal die Fläche eines kleineren Quadrats.
Das wäre eine Aufgabe, die Roland stellen könnte ;-)
Jetzt fehlt nur noch die Faltanweisung ...
Danke,
na ja ähnlich wie beim Bildhauen, man knickt alles ab was nicht zur Figur gehört ;-).
Aber ein zündender Gedanke ist mir noch nicht gekommen...
Jetzt vielleicht doch (vielen Dank für den Hinweis auf \(\phi\)), der überstehende Rand wäre bei
\(t = \frac{1}{2} \; \sqrt{2 \; \left(\sqrt{5} + 1 \right)} =\,\sqrt{\phi}\)
abzuknicken.
Ich fahre eine Ecke D die Diagonale hoch, lasse eine Seite durch C laufen so lange die Projektion von D auf BC (die Seite des neuen Quadrates) innerhalb des bewegten Quadrates bleibt (die Seite trifft).
Phi: die goldene Zahl, das göttliche Verhältnis
Hallo,
ich habe es mit GeoGebra versucht.
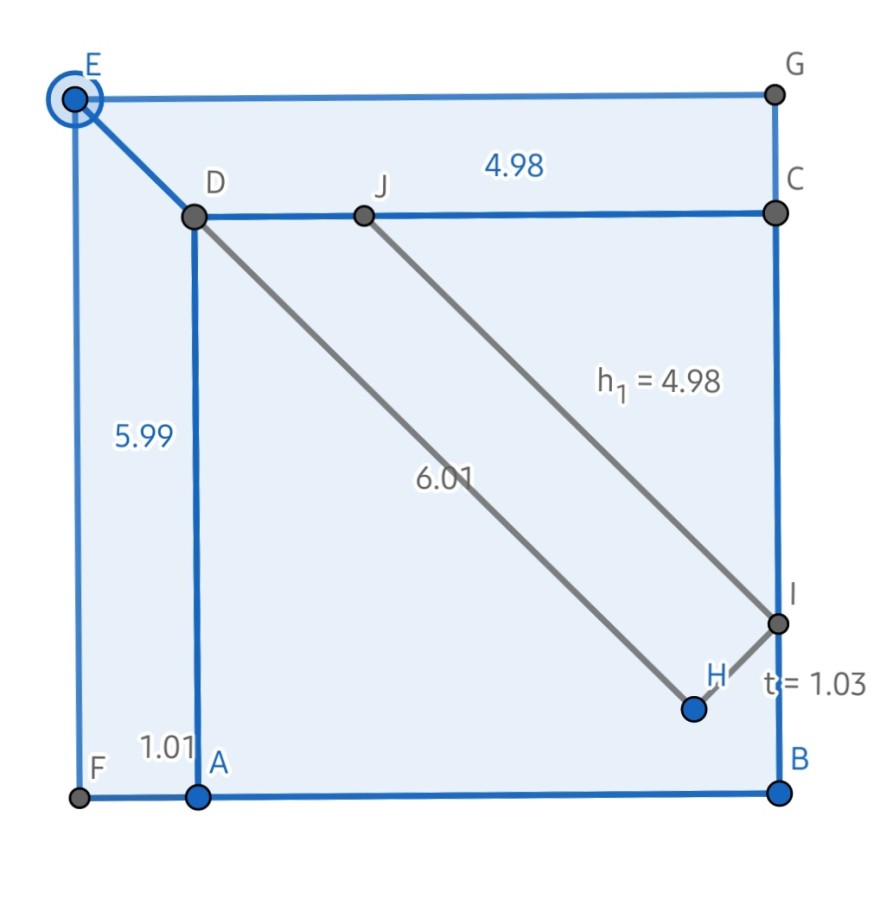
ABCD ist eines der drei gegebenen Quadrate. Wenn man es vergrößern will, muss das angesetzte Stück FADE in das zweite Quadrat hineinpassen. Das obere Stück DCGE wird dann aus dem dritten Quadrat gefaltet.
Bestimmt gibt es noch andere Möglichkeiten.
:-)
Vielen Dank, ich werde es versuchen. :)
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
