Extremstellen berechnen Funktion

Question

Folgende Funktion ist gegeben :

f(x)= $\frac{1}{5}$ x³+2x²+$\frac{21}{5}$x

Aufgabe : Extremstellen und Hoch-bzw.Tiefpunkt berechnen

Bitte mit ausführlichen Rechenweg.

Comments

Warum stellst Du diese Frage zum zweiten Mal?

Answer 1

Hallo,

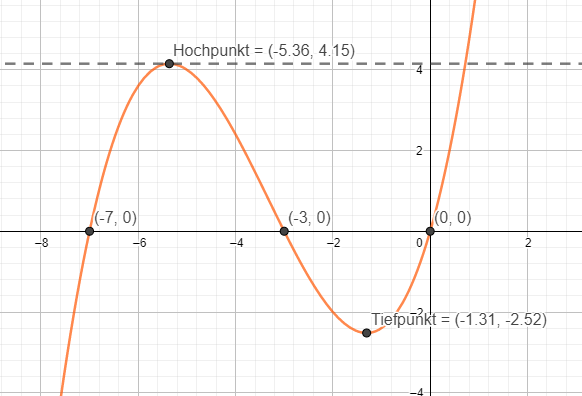
Extremstellen und Hoch-bzw.Tiefpunkt berechnen

Extremstellen sind die x-Koordinaten von Hoch- oder Tiefpunkten. Wenn nach Punkten gefragt wird, musst du auch noch die y-Koordinaten berechnen.

Bei diesen Punkten ist die Steigung = 1. Ableitung gleich null, sie haben also waagerechte Tangenten.

$f(x)=0,2x^3+2x^2+4,2x\\f'(x)=0,6x^2+4x+4,2\\f''(x)=1,2x+4$

$0,6x^2+4x+4,2=0\quad |:0,6\\ x^2+\frac{20}{3}x+7=0\\ \text{pq-Formel anwenden}\\ x_{1,2}=-\frac{10}{3}\pm\sqrt{\frac{100}{9}-7}\\\\ x_1=-\frac{10}{3}-\frac{\sqrt{37}}{3}=-5,36\\ x_2=-\frac{10}{3}+\frac{\sqrt{37}}{3}=-1,31$

Um die y-Koordinaten zu erhalten, setzt du diese Ergebnisse in f(x) ein.

Gruß, Silvia

Comments

Ich danke vielmals.

Ich habe leider kein Taschenrechner zu Hand und kann es daher nicht eingeben :/

---

Du siehst die Ergebnisse in meiner Zeichnung (Hochpunkt, Tiefpunkt).

---

Es tut mir und endlich leid,die Rechnung ist ja darüber,ich danke Ihnen.

Ich bin mir nur unsicher welche Skizze ich dazu zeichnen soll.

---

Du kannst meine übernehmen.

---

Ich habe leider kein Taschenrechner zu Hand

Tipp:

Es gibt kostenlose Taschenrechner-Apps.

:-)