Anspruchsvolle Winkelbestimmung zweier verbundener Dreiecke

Question

Aufgabe: Kniffliges Winkelproblem

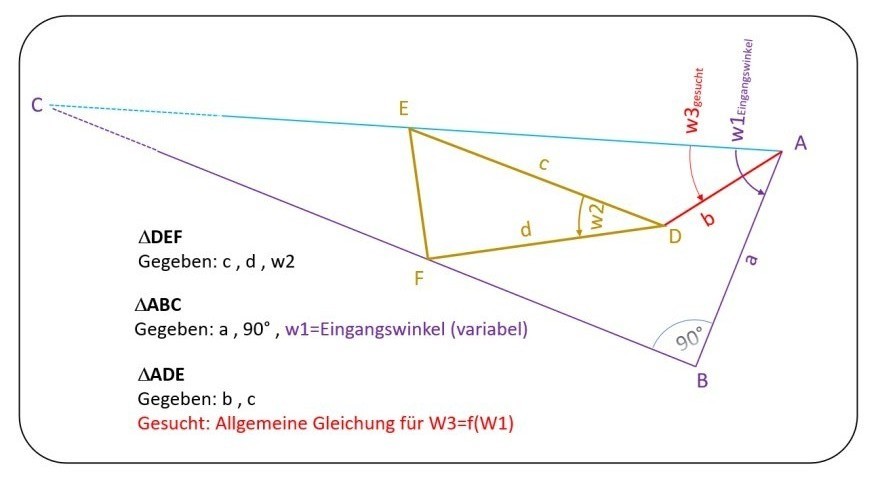
Im Gegebenen System, siehe Skizze, liegen zwei Dreiecke vor, die in sich geometrisch vollständig beschrieben sind.

Zwei Eckpunkte E und F des einen Dreiecks liegen auf den Schenkeln des anderen. Der dritte Eckpunkt ist über eine definierte Länge mit einem Eckpunkt A des anderen Dreiecks verbunden. Der Winkel W1 um den Punkt A ist gegeben. W3 um den Punkt A gesucht. Alle gegebenen Größen liegen in der Skizze beschriftet vor.

Problem/Ansatz:

Es handelt sich um einen Kinematik aus einem technischen Gerät, für welche eine Übertragungsfunktion (Zusammenhang zwischen dem Winkel W1 und W3) gesucht wird.

Wäre w3 gegeben und W1 gesucht, ließe sich das Ergebnis leicht bestimmen. Im vorliegenden Fall (benötigt für weitere Berechnungen) sieht es (für mich) komplizierter aus. Das "System" ist allerdings eindeutig bestimmt. Es muss also EINE Gleichung geben, die den Zusammenhang beschreibt. :)

Wäre super, wenn es dort draußen jemanden gibt, der diese Aufgabe lösen mag und kann. Ich würde mich über eine Herleitung der finalen Gleichung freuen, da ich die allgemeine Form (mit den variablen der Skizze) benötige.

Ich gehe davon aus, dass hier mehrere Gleichungen aufgestellt und über z.B. Einsetzungsverfahren zu einer kombiniert erden können.

Viele Grüße und viel Spaß beim Knobeln :)

Freue mich auf Antwort

Comments

Das wird so nicht in einer Formel zusammenpassen - behaupte ich mal. Es sieht ehr nach einer Optimierungsaufgabe aus.

Mit b,w1 zwingst Du D auf eine Kreisbahn und musst nun zum Segment c,d (abhängig von D) den Punkt mit dem passenden Winkel w2 darüber suchen - nennt man Faßkreis - D wandert also über den Kreisausschnit und stoppt, wenn der Winkel w2 erreicht wird oder auch nicht....

Je nach c,d gibt es auch evtl. bis zu 2 Lösungsmöglichkeiten zu berücksichtigen.

Answer 1

BTW: Hast Du die Frage auch noch in anderen Foren abgestellt?

Wie ich es mir gedacht habe, hab ich keine geschlossene Lösung gefunden.

Ich hab mir die Locus-Kurven der Punkte D_t, F_t, E_t erstellt, wo bei ich nur einen Schnittpunkt F_t betrachtet habe - ggf. müsste man auch den 2ten möglichen Schnittpunkt heranziehen, ob der noch was beiträgt, wenn diese Auswahl ins leere greift. Hab ich nicht näher untersucht...

Dann kann ich zumindest eine numerische Lösung finden.

F_t ist auf der Kante BC festgetackert und D_t läuft im Raduis b um A:
Locus-Kurve E_t schneidet Kante AC (13)

Es wird aber auch Fälle geben, wo man einen Startwert vorgeben muß um die gewünschte Lösung zufinden - halb automatik so zu sagen....

Comments

Guten Morgen,

vielen Dank für die schnelle Antwort. Frage vorab: Mit welcher Software wurde die von Ihnen gezeigte Untersuchung durchgeführt?

Sobald es zwei Lösungen gibt, sollte man doch in der Lage sein, eine Gleichung zu finden, die eben zu diesen beiden Ergebnissen führt (Quadratisch).

Ich werde jetzt etwas Zeit investieren und mit Hilfsstrecken weitere Dreiecke erzeugen, mit denen ich dann ggf. 6 Gleichungen aufstellen kann, entsprechend der Anzahl der vorgegebenen Größen (Konstanten und Variable).

Vielleicht findet noch jemand hier im Forum einen Ansatz, um eine Gleichung (Übertragungsfunktion) zu finden.

Nebenbei: Ich habe diese Frage nur in diesem Forum gestellt. Ich habe bisher noch nie auf diese Möglichkeit zurück gegriffen :)

Viele Grüße und Danke für die dargebotene Auswertung.

---

So, bin wieder online und sehe, daß ich nichts sehe ;-).

Was macht die "Weltwinkel"-Formel?

Die zwei Lösungen kommen nicht aus einer quadratischen Form, sondern, weil ein Kreis (um A) 2 Schnittpunkte mit einer Geraden hat. Gerechnet hab ich übrigens mit GeoGebra....