\(f(x)=a*x^3+b*x^2+c*x+d\)
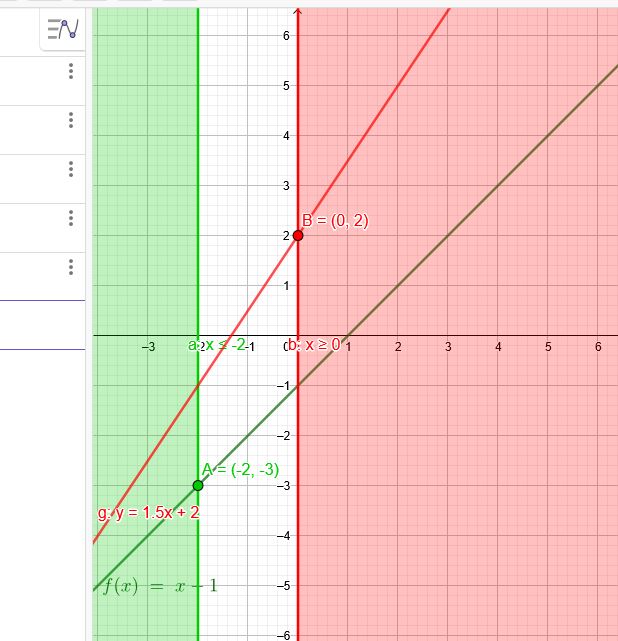
\(A(-2|-3)\)
\(f(-2)=a*(-2)^3+b*(-2)^2+c*(-2)+d\)
1.)
\(a*(-2)^3+b*(-2)^2+c*(-2)+d=-3\)
\(f´(x)=3a*x^2+2b*x+c\)
\(f´(-2)=3a*(-2)^2+2b*(-2)+c\)
2.)
\(3a*(-2)^2+2b*(-2)+c=1\)
\(B(0|2)\)
\(f(0)=a*0^3+b*0x^2+c*0+d\)
3.)
\(d=2\)
\(f´(0)=3a*0^2+2b*0+c\)
4.)
\(c=1,5\)
\(a≈-0,625\) \(b≈-1,75\) \(c=1,5\) \(d=2\)
\(f(x)=-0,625*x^3-1,75*x^2+1,5*x+2\)
