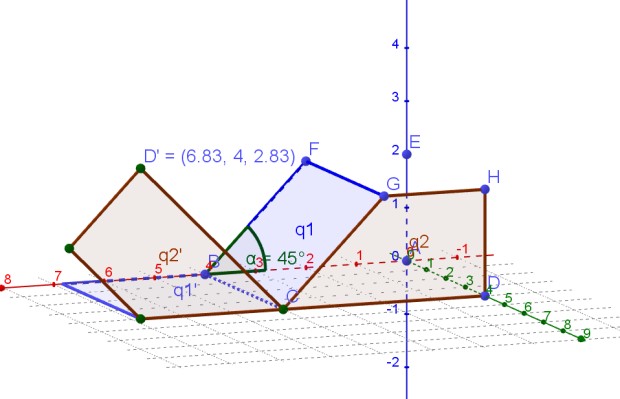
So ich hab hoffentlich die richtigen KO raus gepuhlt und käme mit
Rotation R³-Achse als elementare x,y,z-Achsendrehungen
auf
R_g:To(g(0)) D_x-1 D_y-1 Do((0,0,1),φ) D_y D_x To(-g(0))
\(\small R_g \, := \, \left(\begin{array}{rrrr}\frac{-1}{2} \; \sqrt{2}&0&\frac{1}{2} \; \sqrt{2}&2 \; \sqrt{2} + 4\\0&1&0&0\\\frac{-1}{2} \; \sqrt{2}&0&\frac{-1}{2} \; \sqrt{2}&2 \; \sqrt{2}\\0&0&0&1\\\end{array}\right)\)
Punktauswahl homogene Koordinaten
\(\scriptsize U_H \, := \, \left\{ \left(\begin{array}{r}2\\4\\2\\1\\\end{array}\right), \left(\begin{array}{r}0\\4\\0\\1\\\end{array}\right), \left(\begin{array}{r}4\\4\\0\\1\\\end{array}\right) \right\} \to \left\{ \left(\begin{array}{r}2 \; \sqrt{2} + 4\\4\\0\\1\\\end{array}\right), \left(\begin{array}{r}2 \; \sqrt{2} + 4\\4\\2 \; \sqrt{2}\\1\\\end{array}\right), \left(\begin{array}{r}4\\4\\0\\1\\\end{array}\right) \right\} \)