Wie berechnet man den Flächeninhalt zwischen zwei Funktionen bestimmen, ohne Angabe der Funktionen?

Question

Aufgabe:

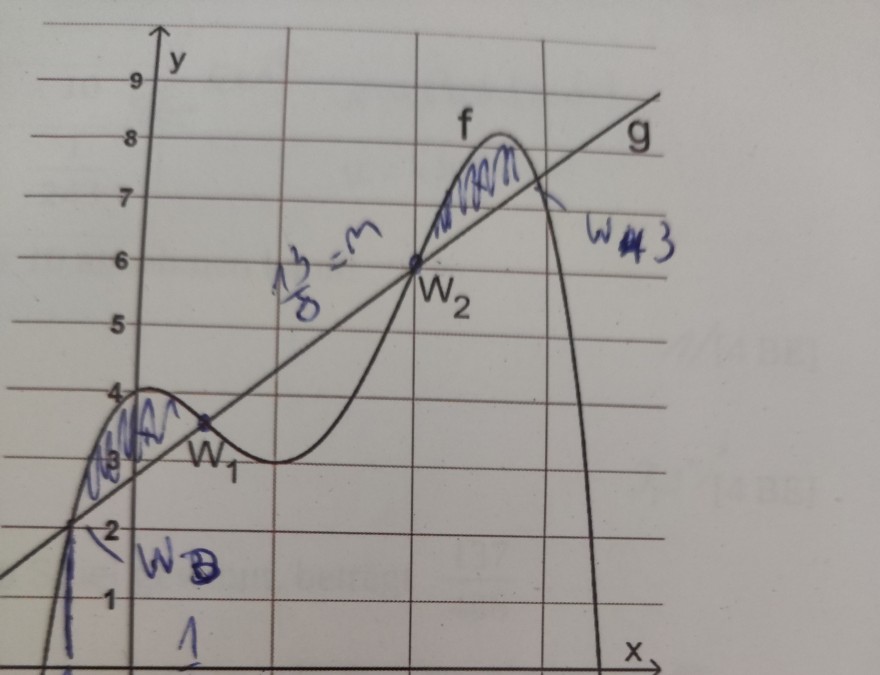
Vergleiche die Inhalte der beiden äußeren Flächen

Problem/Ansatz:

Meine Idee ist es für beide Funktionen die Funktionsgleichungen zu ermitteln. Bei g(x) habe ich die Geradengleichung aufgestellt g(x)= 13/8 * x +2.75 , welche auch passt, meine jetzige Idee war es genug Bedingungen zu finden, um die Funktion f(x) herauszufinden,jedoch fehlen mir jedoch passende Bedingungen, um die Funktion darzustellen und ohne die Funktion kann ich auch nicht den Flächeninhalt der eingeschlossenen Flächen ermitteln.

Ich weiß jetzt nicht ,wie das mit dem Uploaden ist, aber die Wendepunkte der Funktion f(x) sind, W1(0.5/f(0.5)) und W2(2/f(2)) und die Steigung der Geraden g beträgt 13/8.

Comments

Wieviel Gleichungen kannst du aufstellen?

Answer 1

Du brauchst für eine Funktion 4. Grades 5 Bedingungen

f(0.5) = 3.5625
f''(0.5) = 0
f(2) = 6
f''(2) = 0
f(0) = 4 würde ich noch als einfache Bedingung dazu nehmen

Damit komme ich auf die Funktion

f(x) = - 1·x^4 + 5·x^3 - 6·x^2 + x + 4

Skizze

~plot~ -1x^4+5x^3-6x^2+x+4;13/8x+2.75;[[-1|4|-1|9]] ~plot~

Das sieht eigentlich recht gut aus.

Comments

Danke, habe versehentlich mit einer Funktion dritten Grades gerechnet.

---

Wenn eine Gerade eine Funktion an 4 Stellen schneidet, dann muss die Funktion mind. vom Grad 4 sein. Kann man sich eigentlich recht leicht merken.

Oder wenn eine Funktion 3 Extrempunkte hat, muss sie mind. vom Grad 4 sein.

Answer 2

f sieht aus wie eine ganzrationale Funktion 4. Grades, also

f(x)=ax^4 +bx^3+cx^2+dx+e

Die Wendepunkte liefern f''(0,5)=0 und f''(2)=0

und weil sie auf der Geraden liegen ist f(0,5)=g(0,5)

und f(2)=g(2) und was weiß man über W0 und W3 ?

Comments

Über W0/3 weiß man nichts,war nur eine missverständliche Markierung. Es sollte einfach nur die Schnittstelle darstellen

---

Jedoch habe ich die ganze Zeit mit einer Funktion dritten Grades gerechnet,habe mich dort wohl vertan.