Aufgabe:
Leiten Sie die Funktionen mit der Kettenregel ab und vereinfachen Sie sie anschließend.
Problem/Ansatz:
Die Ableitungen habe ich schon gebildet. Allerdings habe ich beim Vereinfachen noch Probleme und würde mich daher über Hilfe freuen.
Ich habe die Funktionen bei der Aufgabe nicht abgetippt, weil ich teilweise nicht ganz wusste wie ich das mit der Tastatur machen kann.
Ist der bisherige Lösungsansatz richtig?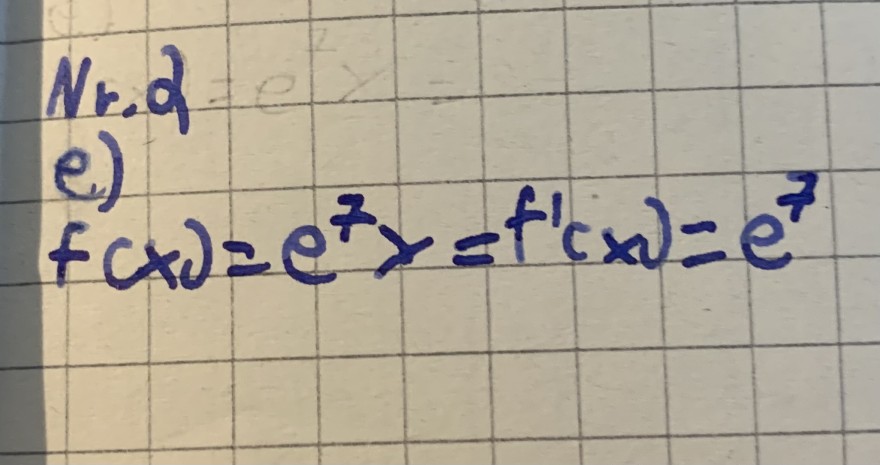
Text erkannt:
Nr.,
\( f(x)=e^{7} x=f^{\prime}(x)=e^{7} \)

Text erkannt:
\( \begin{array}{l}\text { f) } \\ f(x)=e^{2 x^{2}}+x=f^{\prime}(x)=2 e^{2} x+1 \\ \text { f) } \\ \text { h) } \\ f^{\prime}(x)=4 e^{3-4 x}=f^{\prime}(x)=-4 \\ \frac{1}{2} e^{\frac{1}{5} x+2} \Rightarrow f^{\prime}(x)=\end{array} \)
Und bei f wusste ich die Ableitung leider auch nicht.