Aufgabe:
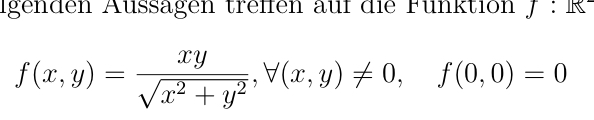
Text erkannt:
\( f(x, y)=\frac{x y}{\sqrt{x^{2}+y^{2}}}, \forall(x, y) \neq 0, \quad f(0,0)=0 \)
Hierbei betrachtet man immer die Stelle (0,0). Dabei ist die Funktion stetig und besitzt die partiellen Ableitungen in Koordinatenachsenrichtung.
Problem/Ansatz:
Ich verstehe aber nicht ganz warum es hier keine partiellen Ableitungen in beliebige Richtungen in (0,0) gibt?
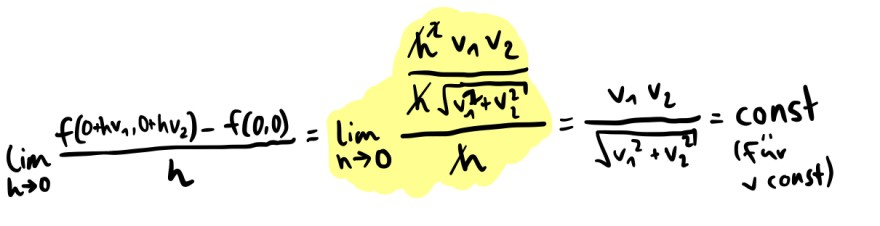
Um das zu prüfen wäre ich so vorgegangen:
Text erkannt:
\( \lim \limits_{h \rightarrow 0} \frac{f\left(0+v_{1}, 0+h v_{2}\right)-f(0,0)}{h}=\lim \limits_{h \rightarrow 0} \frac{\frac{h^{\lambda} v_{1} v_{2}}{K \sqrt{v_{1}^{2}+v_{2}^{2}}}}{h}=\frac{v_{1} v_{2}}{\sqrt{v_{1}^{2}+v_{2}^{2}}}=\underset{\substack{\left(\text { curv }_{v}^{\prime \prime} \text { const }\right)}}{\text { const }} \)
Wobei v = (v1,v2) einfach ein Vektor beliebiger Richtung ist.
Wo liegt mein Fehler?