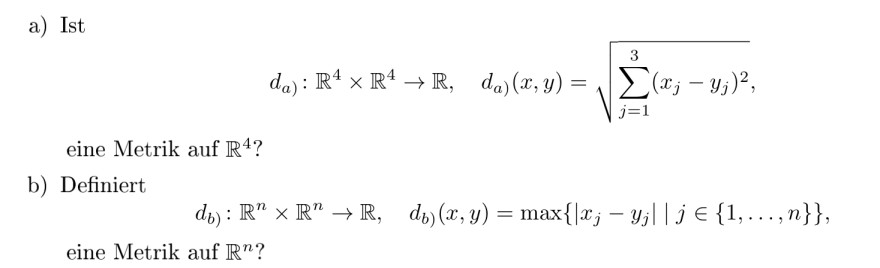
Text erkannt:
a) Ist
\( d_{a)}: \mathbb{R}^{4} \times \mathbb{R}^{4} \rightarrow \mathbb{R}, \quad d_{a)}(x, y)=\sqrt{\sum \limits_{j=1}^{3}\left(x_{j}-y_{j}\right)^{2}} \)
eine Metrik auf \( \mathbb{R}^{4} \) ?
b) Definiert
\( d_{b)}: \mathbb{R}^{n} \times \mathbb{R}^{n} \rightarrow \mathbb{R}, \quad d_{b)}(x, y)=\max \left\{\left|x_{j}-y_{j}\right| \mid j \in\{1, \ldots, n\}\right\}, \)
eine Metrik auf \( \mathbb{R}^{n} \) ?
Zu a): Ich weiß aus der Vorlesung, dass d(x,y) eine Metrik wäre, wenn der Endwert der Summe 4 und nicht 3 wäre, gilt das aber auch in diesem Fall?
Zu b): dass d(x,y)=d(y,x), d(x,x)=0, d(x,y)>0 für x≠y kann man ja relativ leicht zeigen. Wie kann ich aber die Dreiecksungleichung zeigen?