Wie finde ich eine Funktion in Q[x] 3ten Grades die aber nur durch 3 Punkte geht?

Question

Aufgabe:

Konstruieren Sie ein Polynom f, so dass
f(1) = 7, f(2) = 5 und f(3) = 6, grad(f)= 3 in Q[x],

Problem/Ansatz:

habe das Interpolationspolynom berechnet, dieses ist jedoch vom Grad 2. Das sieht man auch schon vor dem Kürzen (Siehe Bild)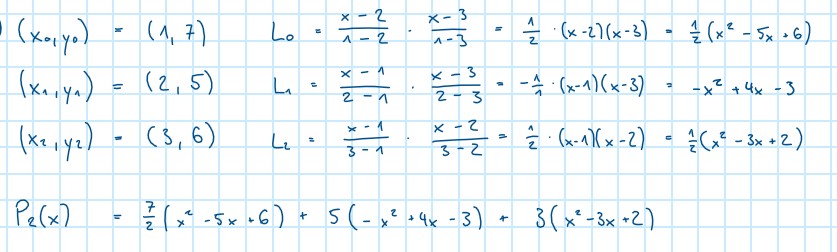

Text erkannt:

\( \begin{array}{l}\left(x_{0}, y_{0}\right)=(1,7) \quad L_{0}=\frac{x-2}{1-2} \cdot \frac{x-3}{1-3}=\frac{1}{2} \cdot(x-2)(x-3)=\frac{1}{2}\left(x^{2}-5 x+6\right) \\ \left(x_{1}, y_{1}\right)=(2,5) \quad L_{1}=\frac{x-1}{2-1} \cdot \frac{x-3}{2-3}=-\frac{1}{1} \cdot(x-1)(x-3)=-x^{2}+4 x-3 \\ \left(x_{2}, y_{2}\right)=(3,6) \quad L_{2}=\frac{x-1}{3-1} \cdot \frac{x-2}{3-2}=\frac{1}{2} \cdot(x-1)(x-2)=\frac{1}{2}\left(x^{2}-3 x+2\right) \\ P_{2}(x)=\frac{7}{2}\left(x^{2}-5 x+6\right)+5\left(-x^{2}+4 x-3\right)+3\left(x^{2}-3 x+2\right)\end{array} \)

Wie bringe ich es auf Grad 3 und was hat Q[x] mit dem ganzen zu tun?

Comments

Addiere (x - 1)·(x - 2)·(x - 3).

Answer 1

Nimm einfach \((x_3,\:y_3)=(a,\:b)\) (das geht aber nicht immer) oder multipliziere das Polynom zweiten Grades mit einem beliebigen Linearfaktor \((x-c)\) (das geht immer). Mit \(\text{Q}[x]\) ist gemeint, dass es hier nur um Polynome mit rationalen Koeffizienten geht. Dies schränkt die Wahl von \(a,\:b\) oder \(c\) ein.

Comments

Aldo wäre f =(x-c)*P2(x)?

---

Nun, darüber muss ich noch mal nachdenken. Versuch es derweil mal mit dem ersten Weg.

Answer 2

Setze einfach \(f(0)=0\). Dann hat dein Polynom die Gestalt

$$f(x) = x(ax^2+bx+c)$$

Nun bestimme mit einer dir angenehmen Methode das Interpolationspolynom

$$f(x) = 2x^3 - \frac{21}2 x^2 + \frac{31}2 x$$

Zur Überprüfung siehe hier .

Comments

warum setzt du f(0) = 0? Das gesuchte Polynom muss muss ja nicht zwingend durch den Nullpunkt gehen

Ausserdem, wenn ich \(f(x) = x(ax^2+bx+c)\) setze bekomme ich \(f(x) = 3/2x^3+13/2x+12)\)

---

Wenn du durch 3 Punkte interpolierst, hat das Interpolationspolynom höchstens den Grad 2.

Du willst aber ein Polynom 3. Grades haben. Also musst du einen weiteren Punkt wählen, der nicht auf der Parabel durch deine 3 gegebenen Punkte liegt (andernfalls bekommst du wieder dasselbe Polynom 2. Grades).

Ich habe f(0)= 0 einfach willkürlich gewählt, weil so das Zielpolynom besonders einfach aussieht und das Absolutglied somit schon eindeutig bestimmt ist.

Das von dir angegebene Polynom 3. Grades geht offensichtlich nicht durch (0,0) und kann daher dem Ansatz \(x(ax^2+bx+c)\) nicht entsprechen.

---

warum setzt du f(0) = 0? Das gesuchte Polynom muss muss ja nicht zwingend durch den Nullpunkt gehen

Deine Frage war: "Wie finde ich EINE Funktion"!

Mit der Annahme f(0) =0 findet man EINE.

Mit der Annahme f(0) =1 findet man eine ANDERE.

Mit der Annahme f(0) =777 findet man NOCH EINE ANDERE.