Den wievielten Teil des regelmäßigen Zwölfecks deckt das Quadrat ab?

Question

Löse mit möglichst geringem Rechenaufwand:

Den wievielten Teil des regelmäßigen Zwölfecks deckt das Quadrat ab?

Comments

Mit gleichseitigen Dreiecken und Quadraten.

Quelle angeben wäre fair:

https://www.spektrum.de/raetsel/welchen-teil-deckt-das-quadrat-ab/2125785

---

Ich frage hier nach einem Ergebnis bei geringerem Lösungsaufwand, als dort vorgeführt wurde. Für veränderte Aufgaben gibt es kein Urheberrecht. Sonst müssten alle Unterrichtswerke voll von Quellenhinweisen sein.

---

Für veränderte Aufgaben gibt es kein Urheberrecht.

Mir geht es gar nicht um rechtliche Fragen, sondern um Respekt.

Nebenbei kann ich keine Änderung gegenüber der Spektrum-Aufgabe erkennen.

:-)

Answer 1

Fläche eines regelmäßigen n-Ecks mit dem Umkreisradius r

$$A_r = n \cdot \frac{1}{2} \cdot r^2 \cdot \sin \left( \frac{360°}{n}\right)$$

Quadratfläche durch Zwölfecksfläche

$$p = \frac{4 \cdot \frac{1}{2} \cdot r^2 \cdot \sin \left( \frac{360°}{4}\right)}{12 \cdot \frac{1}{2} \cdot r^2 \cdot \sin \left( \frac{360°}{12}\right)} \newline p = \frac{4 \cdot \sin \left( 90° \right)}{12 \cdot \sin \left( 30° \right)} \newline p = \frac{4 \cdot 1}{12 \cdot \frac{1}{2}} \newline p = \frac{4}{6} \newline p = \frac{2}{3}$$

Skizze

Geht es noch einfacher?

Comments

Ja, es geht einfacher.

---

Ok. Das siehst du vielleicht so. Wenn ich deine grafische Lösung ansehe bezweifel ich das doch sehr stark.

Offensichtlich bedeutet einfacher Rechenaufwand bei uns beiden doch etwas anderes.

---

Lies bitte meinen Kommentar oberhalb deiner Antwort.

---

Hab ich und ich bleibe dabei das meine Antwort um ein Vielfaches leichter ist und mit weniger Rechenaufwand auskommt.

Answer 2

Zwei Drittel.

Setzen wir den Umkreisradius gleich 1, so hat das Quadrat den Flächeninhalt    Q = 4 · cos(45°) · sin(45°) = 2 · sin(90°) = 2

und das Zwölfeck :    Z = 12 · cos(15°)  · sin(15°) = 6 · sin(30°) = 3

Folglich   Q / Z = 2 / 3

Comments

Deine Zeile

Setzen wir den Umkreisradius gleich 1, so hat das Quadrat den Flächeninhalt   Q = 4 · cos(45°) · sin(45°) = 2 · sin(90°) = 2

hätte auch lauten können

Setzen wir den Umkreisradius gleich 1, so hat das Quadrat die Diagonalenlänge 2 und den Flächeninhalt 2.

Es ging doch um geringen Rechenaufwand.

z,.B. mit dieser Aufteilung

---

Die graphische Lösung ist schön. Aber sie erfordert doch auch noch Überlegungen, die nicht so gaaanz ohne rechnerische Überlegungen auskommen. Anschauen allein genügt nicht - oder ?

"Gerechnet" habe ich wirklich auch nicht viel.

---

rumar: Ich habe doch genau geschrieben, was ich zu aufwändig finde.

---

Um die *graphische Lösung" nachzuvollziehen, kam ich doch noch ziemlich ins Rechnen (mit den Hilfsgrößen  c = cos(30°) = √(3) / 2  und  s = sin(30°) = 1 / 2  für die Katheten des kleinen rechtwinkligen Dreiecks). Kannst du uns verraten, wie du diese Zeichnung liest und daraus das Flächenverhältnis ermittelst ?

---

Es ist zu zeigen, dass die schwarz-orange Flächen zusammen halb so groß sind wie das Quadrat.

Die Seitenlänge des 12-Ecks sei 1.

Die Katheten eines schwarzen Dreiecks sind dann ½ und ½√3. Alle acht schwarzen Dreiecke haben den Flächeninhalt √3.

Die orangen Rechtecke 4•½•1=2.

Schwarz-orange: 2+√3

Nun das Quadrat:

Weiß: 1^2=1

Grau: 4•(½√3)^2=3

Gelb: 4•1•½•√3=2√3

Quadrat insgesamt: 4+2√3=2•(2+√3)

Das ist auch nicht einfach.

Da finde ich die Lösung im "Spektrum" einfacher.

---

Danke Monty.

Aber das sieht doch auch noch arg nach etlichen Rechnungen aus.

Und: könntest du einen Link zum Spektrum-Artikel angeben ?

---

Und: könntest du einen Link zum Spektrum-Artikel angeben ?

Guck mal in meinen Kommentar ganz oben direkt unter Rolands Aufgabe.

:-)

---

Mal ernsthaft. Einfach wird hier wohl von Person zu Person verschieden ausgelegt.

rumar und meine Antwort sind um ein Vielfaches einfacher als die 2 unterschiedlichen grafischen Lösungen und vermutlich auch noch für jeden Hauptschüler einfacher zu verstehen.

Bevor man in Spektrum die Dreiecke und Quadrate gezeichnet oder gezählt hat und damit dann auch noch gerechnet hat ist man bei unseren Lösungen aber schon lange fertig.

Ich würde bei meiner Lösung ein Kürzen/Streichen von 1/2 * r^2 ohnehin nicht wirklich als rechnen zählen. Dort wird nichts gerechnet sondern nur gleiche Faktoren gestrichen.

---

Ich beziehe mich auf den folgenden Kommentar von rumar;

Um die *graphische Lösung" nachzuvollziehen, kam ich doch noch ziemlich ins Rechnen (mit den Hilfsgrößen c = cos(30°) = √(3) / 2  und s = sin(30°) = 1 / 2  für die Katheten des kleinen rechtwinkligen Dreiecks). Kannst du uns verraten, wie du diese Zeichnung liest und daraus das Flächenverhältnis ermittelst ?

Offensichtlich hat rumar erkannt, dass hier ein Winkel der Größe 30° eine Rolle spielt. Auch hat er die Seitenlänge des Zwölfecks als Längeneinheit gewählt. Dann hätte er auch erkennen können, dass eine Teilfigur ein halbes gleichseitiges Dreieck ist. Zu meiner Zeit (vor 1966) kannten die meisten Schüler die Höhe im gleichseitigen Dreieck (insbesondere mit der Seitenlänge 1) noch auswendig. Dann sind alle Flächen meiner Skizze schnell (zu meiner Zeit im Kopf) bestimmt und es geht noch um den Quotienten (6+3√3)/(4+2√3).

---

"Dann hätte er auch erkennen können, dass eine Teilfigur ein halbes gleichseitiges Dreieck ist."

Natürlich habe ich das auch sofort erkannt. Ist es dann deiner Meinung nach falsch, auch noch auf die Winkel und die entsprechenden trigonometrischen Werte hinzuweisen ? Ich muss mich ja dann nachher mit gar keinen Wurzeltermen rumschlagen (dank Doppelwinkelformel).

OK, schönen Tag auch noch ...

---

Hallo zusammen !

Hier jetzt noch meine kurze Notation der Lösung gemäß Spektrum-Artikel:

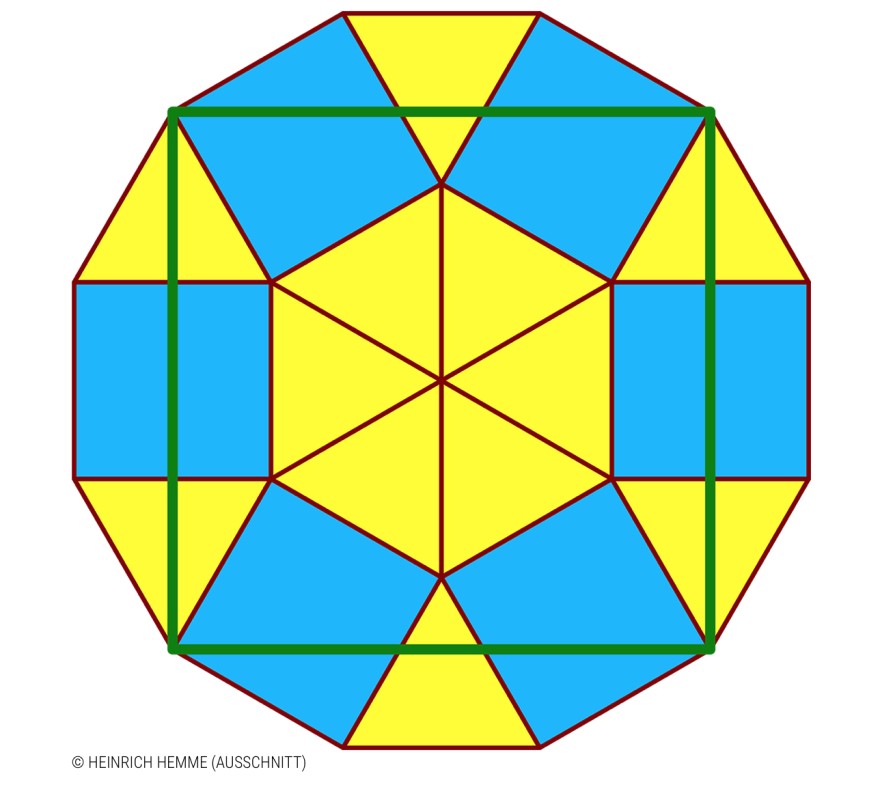
Bezeichnungen für Flächeninhalte:

Z :   Zwölfeck

A :   (großes) Quadrat

Q :  (kleines) blaues Quadrat

D :  (kleines) gelbes Dreieck

Dann gilt:

Z = 6 Q + 12 D

Z - A =  4 · \((\frac{Q + 2 D}{2}) \) =  2 Q + 4 D = \( \frac{ Z}{ 3} \)

also   A =  Z - \( \frac{ Z}{ 3} \) =   \( \frac{ 2}{ 3} \) Z

Dabei komme ich ganz ohne Wurzeln, Winkel, Sin- und Cosinüsse aus ...

Answer 3

Hallo Roland,

\(A_{\text{Zwölfeck}}=(2+\sqrt{3})\cdot 3a^2\\ A_{\text{Quadrat}}=((1+\sqrt{3})\cdot a)^2\\\)

Verhältnis:

\(\displaystyle \frac{(4+2\sqrt{3})a^2}{(2+\sqrt{3})\cdot 3a^2}=\frac{4+2\sqrt{3}}{6+3\sqrt{3}}=\frac{2(2+\sqrt{3})}{3(2+\sqrt{3})}=\frac{2}{3}\)

Gruß, Silvia

Comments

Noch geringer wäre der Rechenaufwand für a=1. Die Wahl der Längeneinheit ist frei, da es um ein Flächenverhältnis geht. Außerdem denke ich an diese Aufteilung: