Gegeben sind die linearen Funktionen f durch y= f(x)= 0,5x+8 und A(1|2) und B(2|9)
1. Die Punkte A und B liegen auf einer Parabel mit der Funktionsgleichung y= x^2+px+q. Bestimme p und q.
A(1|2)
2= 1^2+p*1+q →1.) p+q=1
B(2|9)
9= 2^2+p*2+q →2.) 2p+q=5
Löse nun das Gleichungssystem:
2.)-1.) p=4 in 1.) 4+q=1 → q=-3
y= x^2+4x-3
2. Zeige rechnerisch, dass der Punkt B auf dem Graphen der Funktion f liegt.
B(2|9)
9= 2^2+4*2-3=9 ✓
3. Eine Funktion g ist durch die Gleichung y=g(x)=x^2+4x-3 gegeben. Die Graphen der Funktion f und g haben einen weiteren Punkt C gemeinsam. Ermittle die Koordinaten von C
x^2+4x-3=0,5x+8 |-0,5x+3
x^2+3,5x=8+3=11
\(x^2+ \frac{7}{2} x=11 \)
\((x+ \frac{7}{4})^2=11+(\frac{7}{4})^2=\frac{176}{16} + \frac{49}{16}= \frac{225}{16} | \sqrt{~~ }\)
1.)
\(x+ \frac{7}{4}= \frac{15}{4} \)
\(x_1= 2 \) \(y_1=0,5*2+8=9\)
2.)
\(x+ \frac{7}{4}= -\frac{15}{4} \)
\(x_2= - 5,5 \) \(y_2=0,5*(- 5,5)+8=5,25\)
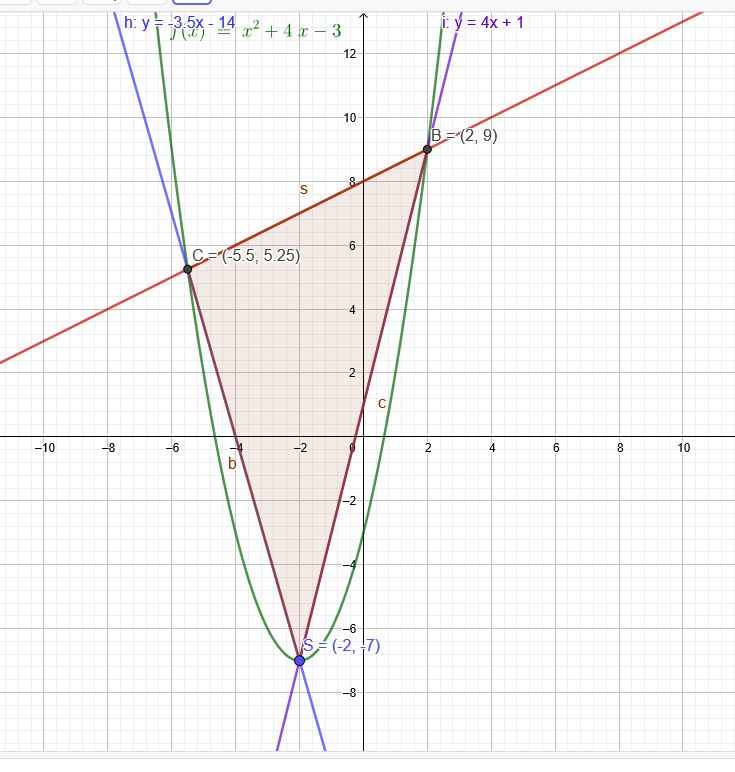
4. Die Punkte B, C und der Scheitelpunkt S der Funktion g bilden ein Dreieck, von dem ein Teilstück unterhalb der x-Achse liegt.
Berechnung des Scheitelpunkts:
\(y=x^2+4x-3\)
\(y´=2x+4\)
\(2x+4=0\)
\(x=-2\) \(y(-2)=(-2)^2+4*(-2)-3=-7\)
Bestimme nun die Geradengleichungen durch S und C und durch S und B
Die Schnittpunkte mit der x-Achse geben die Punkte der Dreiecksbasis.
Berechne die Länge dieser Basis. Die Höhe des Dreiecks ist der |y-Wert| des Scheitelpunktes.
A=...