Welche Matrix Vektor Schreibweise ist richtig?

Question

Aufgabe: Matrix Vektor Schreibweise

Problem/Ansatz:

Hallo, ich bin mir bei diesem Beispiel nicht ganz sicher was die Vektor Matrix Schreibw. ist.

Grundsätzlich geht es mit um die Matrix A.

Normal ist die Formel ja gegeben wie im Bild ersichtlich:

Jedoch gilt ja auch dass man die Vorfaktoren von x1^2 in das obere linke Eck und von x2^2 in das untere rechte Eck schreibt.

Wenn ich nach der gegeben Formel gehe führt dies bei den Eigenwerten zu Problemen, daher frage ich mich, ob man hier die Schreibweise 1. verwenden muss?

Kann mit hier jemand helfen? Danke

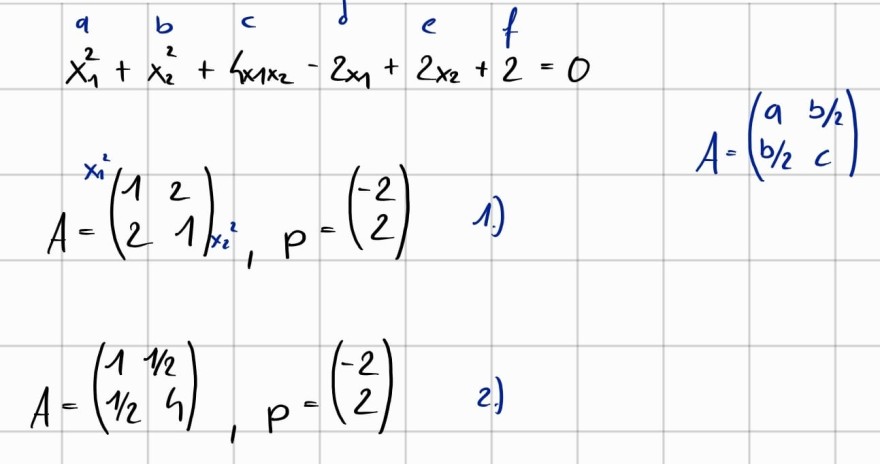
Text erkannt:

\( \begin{array}{l}\left.A=\left(\begin{array}{ll}1 & 2 \\ 2 & 1\end{array}\right) x_{2}^{2}, p=\left(\begin{array}{c}-2 \\ 2\end{array}\right) \quad 1\right) \\ A=\left(\begin{array}{cc}a & b / 2 \\ b / 2 & c\end{array}\right) \\ A=\left(\begin{array}{ll}1 & 1 / 2 \\ 1 / 2 & 4\end{array}\right), p=\left(\begin{array}{c}-2 \\ 2\end{array}\right) \quad \text { 2) } \\\end{array} \)

Answer 1

So ein Durcheinander - was ist der Krakel vor x1x2?

Deine a,b,c Nummerierung von A trifft nicht zu...

\(A=\left(\begin{array}{rr}a&\frac{1}{2} \; c\\\frac{1}{2} \; c&b\\\end{array}\right)\)

Man kann ja auch das Matrizenprodukt ausrechnen - dann sollte die Quadrikgleichung auch raus kommen!

eine Zusammenfassung siehe

https://www.geogebra.org/m/BpqJ28eP#material/jybmgrce

Comments

Sorry :D das ist eine vier

Answer 2

Gemäß deinen Bezeichnungen ist$$A=\left(\begin{array}{cc}a&c/2\\c/2&b\end{array}\right)$$Auf der Diagonalen stehen die Koeffizienten der Quadrate,

an den Positionen (1,2) und (2,1) der halbierte Koeffizient von \(x_1x_2\).

Comments

Danke für deine Antwort

Also steht hier a, b in der Hauptdiagonale

und jeweils c halbiert in der Nebendiagonale?

Ich dachte immer, dass man nach der Formel geht wo b immer halbiert wird aber man muss nach nach den x^2 ten und den x1x2 richten?

Dann ist 1.) richtig formuliert oder?

---

Ja. Dann musst du aber deine Vorgabe als

\(ax_1^2+bx_1x_2+cx_2^2+\cdots\) schreiben.

---

Das wäre dann bei 2.) so oder?

Ich schreibe es nochmal schöner auf fürs Verständnis

---

Es ist ganz einfach:

\(ax_1x_1+bx_1x_2+cx_2x_2+...\)

\(=a\cdot x_1x_1+b/2\cdot x_1x_2+b/2\cdot x_2x_1+c\cdot x_2x_2+ ...\).

An der Stelle (1,1) steht also \(a\),

an den Stellen (1,2) und (2,1) steht \(b/2\) und

an der Stelle (2,2) steht \(c\).

---

Alles klar vielen Dank!

Ich hab das jetzt nochmal an zwei Beispielen demonstriert:

So ist das dann richtig ja?

Text erkannt:

\( \begin{array}{c}x_{1}^{2}+x_{2}^{2}+4 x_{1} x_{2}-2 x_{1}+2 x_{2}+2=0 \\ A=\left(\begin{array}{cc}1 & 4 / 2 \\ 4 / 2 & 1\end{array}\right)=\left(\begin{array}{ll}1 & 2 \\ 2 & 1\end{array}\right)\end{array} \)
\( \begin{array}{l}5 x_{1}^{2}+26 x_{1} x_{2}+5 x_{2}^{2}+62 x_{1}+46 x_{2}+9=0 \\ A=\left(\begin{array}{cc}5 & 26 / 2 \\ 26 / 2 & 5\end{array}\right) \Rightarrow\left(\begin{array}{cc}5 & 13 \\ 13 & 5\end{array}\right)\end{array} \)

---

Ja. So ist es richtig :-)

---

Danke sehr! :)