Servus, ich habe ein folgendes Anliegen. An sich könnte die Aufgabe sehr einfach sein, aber ich bin auch schon viele Jahre aus der Schule raus und hab damit kaum noch Berührungspunkte.
Gegeben ist ein 2D-Koordinatensystem. Auf der X-Achse, lediglich nur der positive Teil, befindet sich irgendwann ein linearer Graph G mit einem positiven Anstieg. Meine Aufgabe dazu lautet, herauszufinden, an welchen Punkten an der X-Achse der Graph welchen Y-Wert annimmt. Ich fertige dazu mal eine Zeichnung an. (Wird aber keine schöne Zeichnung.)
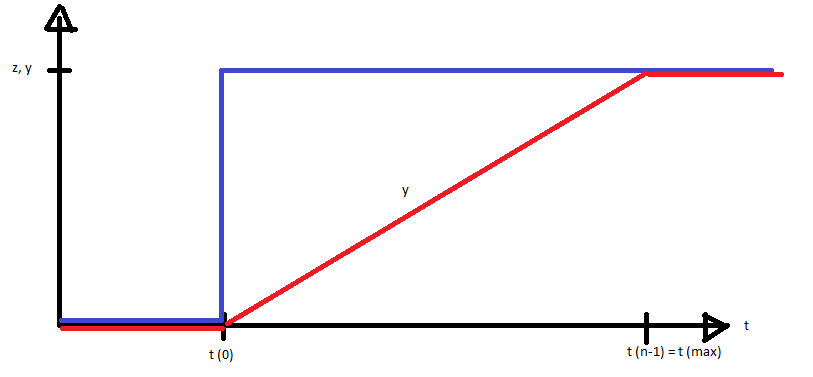
Dabei gilt
- z sei ein maximaler Wert, welcher zur Laufzeit bestimmt werden kann
- y der abzubildende Graph, lediglich von t(0) bis t (n-1)
- t (n) (n = 0,1,2,3,...,n-1) stellen Zeitabschnitte dar
Wie schon oben erwähnt, gilt es herauszufinden, an welchen Punkten t der Wert von y sich ändert. Etwa so:
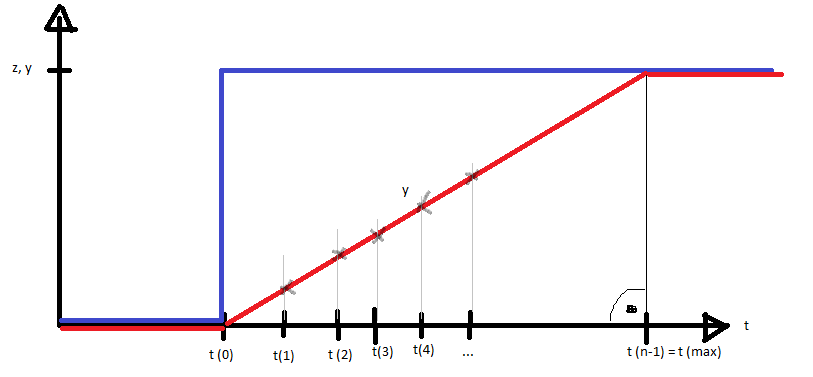
Meine Ansätze waren, da es eine lineare Funktion ähnelt, es nach y = mx+n anzugehen, aber die Werte sind dafür sehr wahrscheinlich nicht (ganz) ermittelbar. n ist bspw. nicht ermittelbar, da zwischen dem Koordinatenursprung und t (0) beliebig viele Punkte dazwischen liegen könnten. Seien es vielleicht nur 10, 145, 9289428648264284 usw.
Mein 2. Ansatz wäre, da t (0..n-1) eine bekannte Gerade ist und auch z bekannt ist, dass dies als Dreieck hergenommen werden kann. Zu t(n-1) sei dies ein 90° Winkel.
Die Idee dahinter wäre also mittels der trigonometischen Formel den Winkel Alpha zu errechen. Das wäre notwendig, damit die einzelnen Höhen zu t ermittelbar wären, indem dann dort die Formel nach z(t) umgestellt werde. Des weiteren kann man so auch kleine Stufen einzeichnen.

Sei b (y) die Hypotenuse, dann kann ich mittels sin(alpha) = a/c = z/t annehmen.
Es sei auch mal folgendes gegeben:
z = 100, t = 10 => für t(0,1,2..) wäre das mal ein Abstand von je 1
Demnach ergibt alpha = arcsin (100/10) = arcsin(10) = 1,57079... + 2,99322i, wobei der imaginäre Teil für mich uninteressant und vielleicht auch störend ist. Aber wenn ich den Winkel bspw. für t(0) zu t(1) einsetze, dann sollte anhand des linearen Graphen der Anstieg, quasi z(t) gleich sein, aber das ist es nicht.
Nach der Formel würde ich z(t) wie folgt errechnen: sin(alpha) * c = a, was aber bei alpha = 1,57079 und c (sagen wir mal konstant 100) dann für a einen Wert von 100 ergäbe, was aber keinen Sinn macht..?
Wie bereits erwähnt, bin ich schon etwas lange draußen und habe keine Idee, wie ich das umsetzen kann. Kann da jemand eine Hilfestellung geben?
Vielen Dank! (: