Aufgabe:
Privatier Karl R. hat die Möglichkeit, ein Unternehmen für 1.000.000 € zu erwerben. Laut Prognose werden Rückflüsse von 35.000 € pro Jahr erwartet, welche jährlich um 3% wachsen. Die erste Zahlung erfolgt dabei in 15 Jahren.
Zu welchem Zeitpunkt n müssten die Rückflüsse des Unternehmens beginnen, damit Karl R.
zwischen einer Investition in das Unternehmen und einer Investition am Kapitalmarkt zu einem Zinssatz von 5% indifferent ist? (Gehen Sie von der ursprünglichen Auszahlung von 35.000 € aus.)
Dies ist die Formel von der ausgegangen wird:
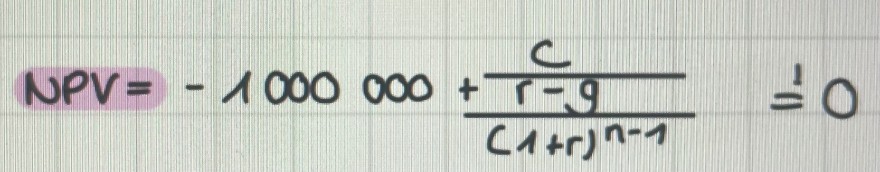
Text erkannt:
\( N P V=-1000000+\frac{\frac{c}{r-g}}{(1+r)^{n-1}}=0 \)
C= 35000 r=0,05 g=0,03
Wie stellt man diese Formel nach n um, sodass man den in der Aufgabe beschriebenen Zeitpunkt erhält?