Aufgabe:
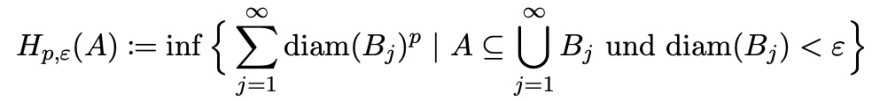
Text erkannt:
\( H_{p, \varepsilon}(A):=\inf \left\{\sum \limits_{j=1}^{\infty} \operatorname{diam}\left(B_{j}\right)^{p} \mid A \subseteq \bigcup_{j=1}^{\infty} B_{j}\right. \) und \( \left.\operatorname{diam}\left(B_{j}\right)<\varepsilon\right\} \)
Problem/Ansatz:
Zeigen Sie: Ist $$ H_p(A)< \infty \rightarrow H_q(A)=0$$ für alle q>p.Ist $$ Hq(A)>0 \rightarrow H_p(A)=\infty $$ für alle p<q mithilfe von $$H_(q,ε)(A) ≤ ε^{q−p} \cdot H_{p,ε}(A) $$.
#Das Epsilon in der Ungleichung geht gegen 0 im GW-Prozess, aber wie schließt man, dass H_p(A) z.B. unendlich ist und vice versa im anderen Fall?
Viele Grüße