Willkommen in der Mathelounge,
du kannst eine solche Funktion auch mit der Produktregel ableiten:
\( f(x)=u(x) \cdot v(x) \Longrightarrow f^{\prime}(x)=u(x) \cdot v^{\prime}(x)+u^{\prime}(x) \cdot v(x) \)
oder kurz geschrieben \( f=u \cdot v \Rightarrow f^{\prime}=u \cdot v^{\prime}+u^{\prime} \cdot v \)
Hier sind
\(u=3x^5\quad u'=15x^4\quad v=e^{2x}\quad v'=2e^{2x}\)
Wenn du die Ableitung gebildet hast, setzt du in sie -0,95 für x ein.
[spoiler]
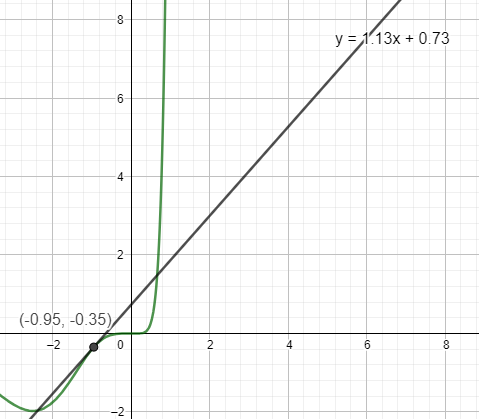
\(f'(x)=3x^5\cdot 2e^{2x}+15x^4\cdot e^{2x}\\ =e^{2x}\cdot (6x^5+15x^4)\\ f'(-0,95)\approx 1,13\)
[/spoiler]
Melde dich, falls du noch Fragen hast.
Gruß, Silvia