Aufgabe:
Ich habe folgende Übungsaufgaben zu lösen und überhaupt keine Ahnung wie das geht. Kann das jemand bitte grundlegend erklären?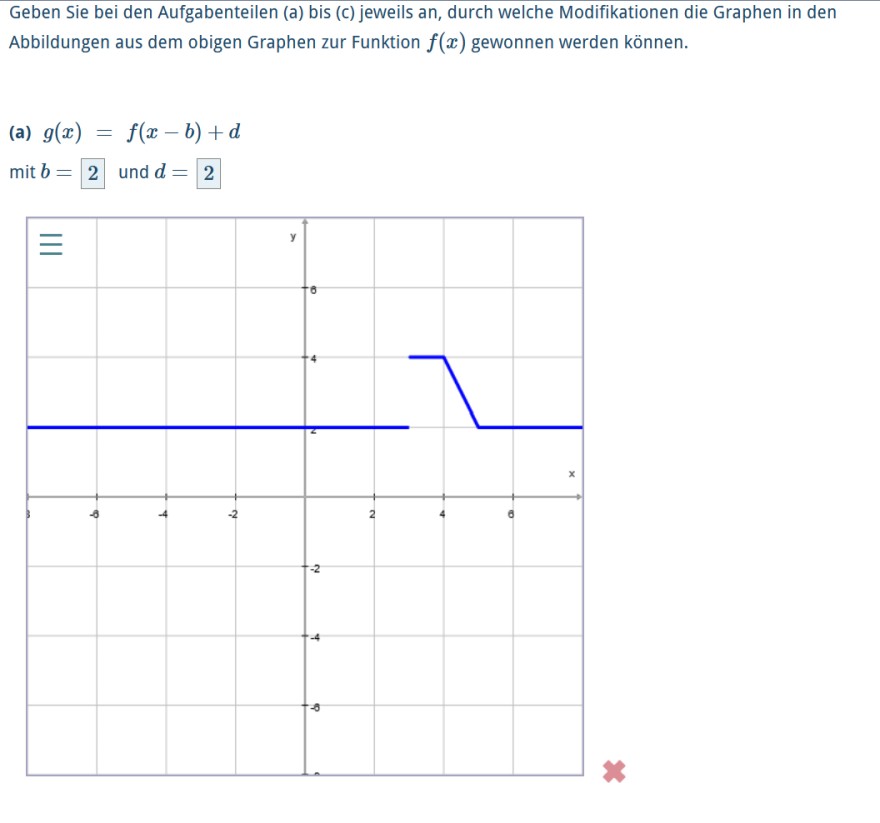
Text erkannt:
Geben Sie bei den Aufgabenteilen (a) bis (c) jeweils an, durch welche Modifikationen die Graphen in den Abbildungen aus dem obigen Graphen zur Funktion \( f(x) \) gewonnen werden können.
(a) \( g(x)=f(x-b)+d \)
mit \( b=2 \) und \( d=2 \)
Text erkannt:
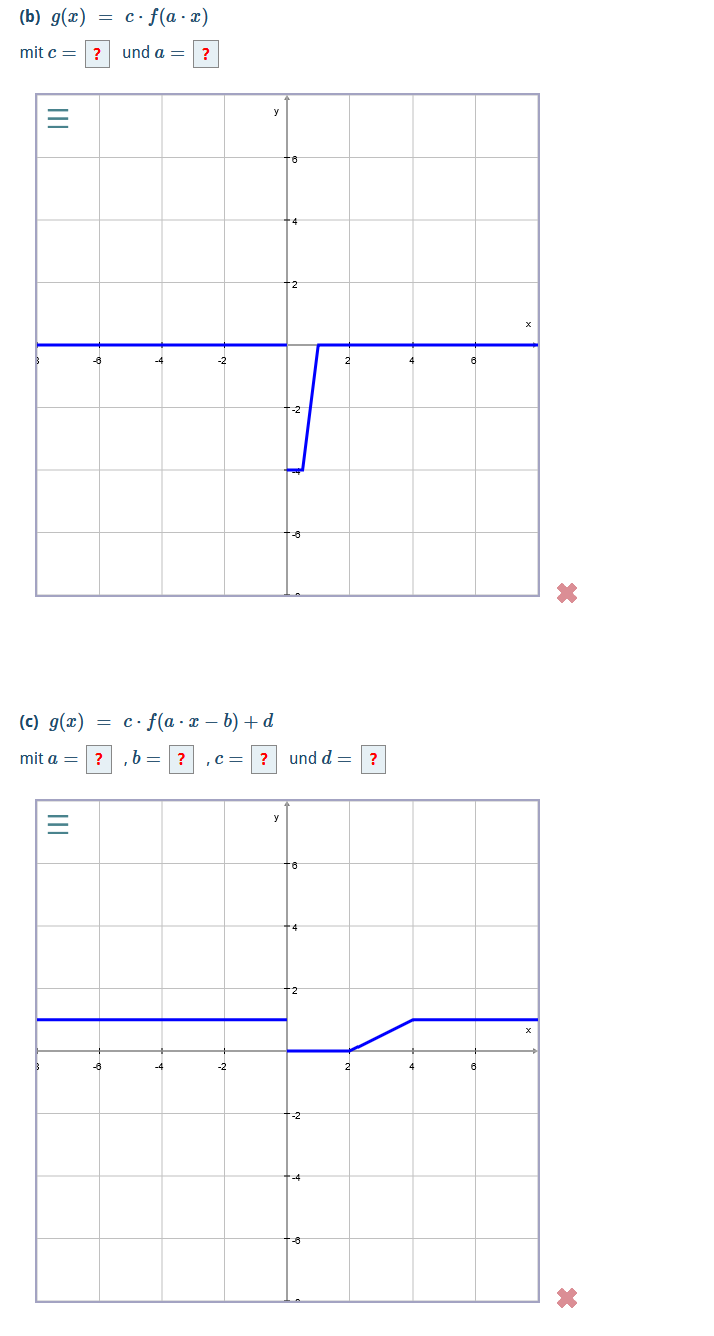
(b) \( g(x)=c \cdot f(a \cdot x) \)
mit \( c= \) ? und \( a= \) ?
(c) \( g(x)=c \cdot f(a \cdot x-b)+d \)
mit \( a=?, b=?, c=? \) und \( d= \) ?

Text erkannt:
(d) Der Graph zu einer Funktion \( f \) soll im Folgenden zunächst an der \( y \)-Achse gespiegelt, danach um das 2 -fache in Richtung der \( y \)-Achse gestreckt werden und anschließend im Koordinatensystem um 4 nach oben verschoben werden.
Geben Sie \( a, b \) und \( c \) ein, damit der Funktionsgraph zu \( g(x)=a f(b x)+c \) dieser Modifikation entspricht:
\( a=?, b=?, c=? \)
(e) Bestimmen Sie \( r>0 \) und \( \varphi \in]-\pi, \pi] \) so, dass für \( f(x)=6 \sin (x)+3 \cos (x) \) gilt: \( f(x)=r \cos (x-\varphi) \).
Es muss gelten: \( \boldsymbol{r}=\boldsymbol{?} \) und \( \varphi=? \)
…
Problem/Ansatz:
