Geben Sie mithilfe der Stellen x1 bis x7 die Intervalle an, in denen der Graph linksgekrümmt bzw. rechtsgekrümmt ist.

Question

Aufgabe:

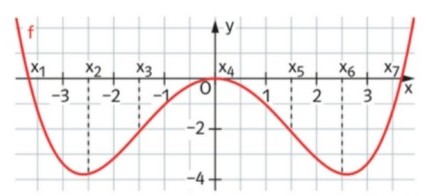
Die Abbildung zeigt den Graphen einer Funktion $\mathrm{f}$.

a) Geben Sie mithilfe der Stellen $x_{1}$ bis $x_{7}$ die Intervalle an, in denen der Graph von f linksgekrümmt bzw. rechtsgekrümmt ist.

b) Der in Fig. 2 dargestellte Graph der Funktion $f$ besitzt die Gleichung $f(x)=\frac{1}{12} x^{4}-\frac{9}{8} x^{2}$. Überprüfen Sie Teil a) rechnerisch.

Problem/Ansatz:

Nr. 1 habe ich bereits gemacht:
- unendlich bis x3 linksgekrümmt
x3 bis x5 rechtsgekrümmt

x5 bis unendlich linksgekrümmt

Nr. 2

glaube ich muss ich erst zwei mal ableiten und dann mit null gleichsetzen (?)

Habe dann als Ergebniss die Wuzel aus 18/8 dass sind -1,5 und 1,5. Aber was heißt das dann?

Answer 1

Das sind die Stellen mit Krümmung $0$, also wo die Krümmung möglicherweise ihre Richtung ändert. Wenn Du richtig gerechnet hast, sind das die Stellen $x_3$ und $x_5$.

Zwischen diesen Stellen gilt: $f''(x)\ge 0\iff$ Graph von $f$ ist linksgekrümmt, analog für $\le 0$ und rechtsgekrümmt. Überprüfe das mit Deinem Ergebnis aus a).

Comments

Achso, also sind das die Stellen -1,5 was x3 ist und 1,5 was x5 ist ?

---

Genau so ist es