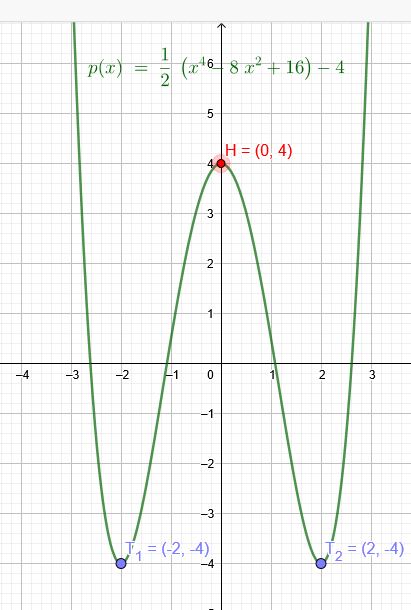
Ein schneller Weg:
\(T_1(-2|-4)\) \(T_2(2|-4)\) \(H(0|4)\)
Ich verschiebe den Graphen um 4 Einheiten nach oben:
(Es sind nun bei \(x=-2\) und \(x=2\) doppelte Nullstellen)
\(T_1´(-2|0)\) \(T_2´(2|0)\) \(H´(0|8)\)
\(f(x)=a*(x+2)^2*(x-2)^2=a*(x^2-4)^2=a*(x^4-8x^2+16)\)
\(H´(0|8)\):
\(f(0)=a*(0^4-8*0+16)=16a=8\) → \(a=\frac{1}{2}\)
\(f(x)=\frac{1}{2}*(x^4-8x^2+16)\)
um 4 Einheiten nach unten:
\(p(x)=\frac{1}{2}*(x^4-8x^2+16)-4\)