Matrixgleichung richtig berechnet

Question

Ist das so richtig gerechnet

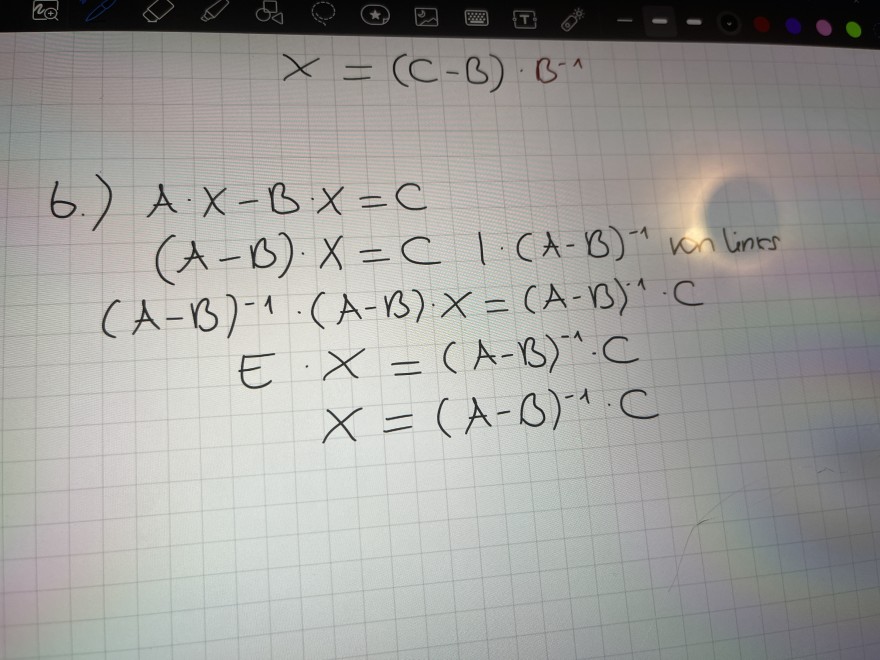
Text erkannt:

\( x=(C-B) \cdot B^{-1} \)
b.)
\( \begin{array}{c} A \cdot X-B \cdot X=C \\ (A-B) \cdot X=C \quad \mid \cdot(A-B)^{-1} \text { ren lines } \\ (A-B)^{-1} \cdot(A-B) \cdot X=(A-B)^{-1} \cdot C \\ E \cdot X=(A-B)^{-1} \cdot C \\ x=(A-B)^{-1} \cdot C \end{array} \)

Answer 1

Ja, wenn A-B invertierbar ist.

Comments

Ist das so korrekt und warum kommt da 2E?

Text erkannt:

c.)
\( \begin{array}{l} A \cdot X-X=X+E 1-X \\ A \cdot x-2 x=E \\ (A-2) x=E \quad \mid \cdot(A-2)^{-1} \text { ven linss } \\ (A-2)^{-1} \cdot\left(A-2 A X=(A-2)^{-1}+E\right. \\ x=(A-2 E)^{-1}+E \end{array} \)

---

Weil 2X =2EX, und so muss es geschrieben werden, weil A-2 geht ja nicht (Matrix minus Zahl).

---

wurde das aber richtig berechnet

---

Nein, rechts muss  \(\cdot\) stehen, nicht \(+\).

---

wieso * und nicht +

---

Weil Du von links multiplizierst.

Wenn Du die Gleichung \(\frac12x=y\) umstellst, entsteht dann \(x=2+y\) oder \(x=2\cdot y\)?

---

stimmt danke

Answer 2

A·X - X = X + E
A·X - 2·X = E
A·X - 2·E·X = E
(A - 2·E)·X = E
X = (A - 2·E)^{-1}