Aufgabe:
(a) Finden Sie die Transformationsmatrizen T und S, welche die folgenden Matrizen mit reellen
Einträgen auf Normalform (vgl. 2.7.9) bringen:
Text erkannt:
\( A=\left(\begin{array}{rrr}1 & 0 & 1 \\ 0 & -1 & 0 \\ 1 & 1 & 1\end{array}\right), \quad C=\left(\begin{array}{rrr}1 & -2 & 5 \\ 3 & 5 & 8\end{array}\right), \quad D=\left(\begin{array}{ll}1 & 2 \\ 3 & 4 \\ 5 & 6\end{array}\right) \)
(b) Geben Sie die Basen an, bezuglich welcher die jeweilige Matrix durch die zugehörige Normalform
beschrieben werden kann. Kontrollieren Sie das durch Proberechnungen.
Hierbei ist zu Erwähnen, dass mit Normalform nicht die Jordan'sche Normalform gemeint ist. Die Normalform wird anders definiert. Die wichtigen Textstellen aus dem Skript tue ich in den Anhang:
2.4.10 Korollar (Einfache Matrixdarstellung einer linearen Abbildung).
Seien \( V, W \) zwei \( K \)-Vektorräume, \( F: V \longrightarrow W \) lineare Abbildung und \( n=\operatorname{dim} V, m=\operatorname{dim} W \), \( r=\operatorname{dim} \operatorname{Im} F \), mit \( n, m, r \in \mathbb{Z}_{+} \). Dann gilt: \( \exists \mathcal{A} \) Basis von \( V \quad \exists \mathcal{B} \) Basis von \( W \) :
\( \mathrm{M}_{\mathcal{B}}^{\mathcal{A}}(F)=\left(\begin{array}{cc}E_{r} & 0 \\ 0 & 0\end{array}\right) \in K^{m \times n} \), wobei \( \mathrm{E}_{r} \) die \( r \)-reihige Einheitsmatrix (und bei \( r=0 \) leere Matrix) ist und jede 0 jeweils eine Nullmatrix von geeignetem Format oder leere Matrix ist.
2.6.16 Bemerkung (Normalform).
Eine Matrix \( \left(\begin{array}{cc}E_{r} & 0 \\ 0 & 0\end{array}\right) \) mit \( r \in \mathbb{Z}_{+} \)wie in 2.6 .15 heißt auch Normalform. Hierbei ist \( \mathrm{E}_{r} \) die \( r \)-reihige Einheitsmatrix (und für \( r=0 \) die leere Matrix) und jede 0 jeweils eine Nullmatrix von geeignetem Format oder leere Matrix.
Problem: Normalformen bei Betrachtung der Ähnlichkeit von Matrizen.
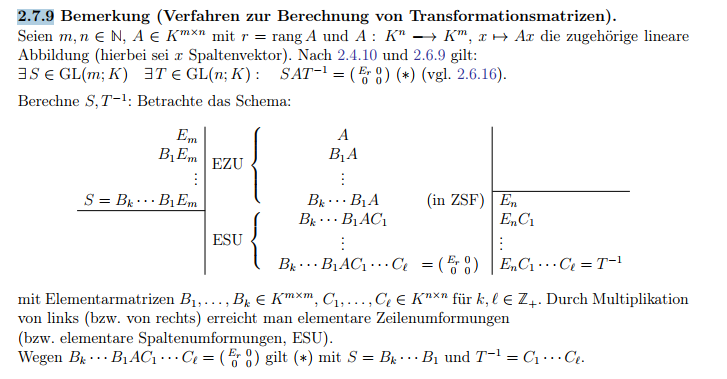
Problem/Ansatz:
Mein Probleme mit der Aufgabe sind folgende:
- Ich verstehe nicht genau was gefragt ist. Ich verstehe was eine Transformationsmatrix ist:
Transformation Matrix is a matrix that transforms one vector into another vector by the process of matrix multiplication. The transformation matrix alters the cartesian system and maps the coordinates of the vector to the new coordinates.
Wikipedia nennt es auch Abbildungsmatrix. Wenn ich jetzt nur die Matrix in eine Transformationsmatrix bringen soll die der Normalform entspricht, warum existieren zwei davon: S und T?
- Kann mir jemand das Verfahren, wie ich die Transformationsmatrix "für doofe" erklären oder mir einen Ratschlag geben wo ich suchen kann um eine gute Erklärung zu bekommen? Ich verstehe das Vorgehen leider vorne und hinten nicht.
- Wenn es nur darum geht die Matrix in eine Einheitsmatrix zu bringen, warum dann dieses komplizierte Vorgehen?
Dinge dich ich versucht habe:
1. Ich habe mich zu Eigenvektoren, Eigenwerten und der Jordan'schen Normalform informiert und mir aus meinen Lektüren wichtig erscheinende Textstellen durchgelesen und habe nun ein grobes Verständnis über Basiswechsel, die mechanismen von Eigenvektoren und Eigenwerten und verstehe warum die Jordan'sche Normalform eine tolle Sache ist. Leider stimmt diese nicht mit der Definition meines Dozenten überein, also musste ich von neuem beginnen.
2. Ich konsultierte das Skript, welches leider für mehr Verwirrung als Klarheit sorgte. Ich kann z.B. mit Bemerkung 2.7.9 absolut nichts anfangen. Das Schema verwirrt mich und ich finde auch leider in meinen Lehrbüchern und im Internet nichts ähnliches zu.
3. Ich habe nach den Begriffen, welche verwendet werden in einer Suchmaschine gesucht um dazu Definitionen und Lösungsansätze zu finden und habe leider nichts gefunden, was zu der Problemstellung passt. Ich habe während meiner Recherche viele neue Informationen ergattert, kriege diese Aufgabe leider immer noch nicht gelöst.
Ich fände es sehr nett, wenn mir das jemand erklären könnte, einen guten Artikel dazu kennt oder einfach Ratschläge geben könnte diese Aufgabe zu lösen. Ich bedanke mich für eure Hilfe im Voraus.
Liebe Grüße
Shoto