Konstruieren von Bildpunkten

Question

Aufgabe: Es sei φ Affinität der affinen Ebene AG(2,R) mit der Achse L = (1, 2) + R(1,−1) und
φ((2, 0))= (4, 1).
a) Konstruieren Sie die Bildpunkte von (0, 0) und (0, 3/2 ).
b) Berechnen Sie t ∈ R und eine (2 × 2)-Matrix M mit φ(x) = t + xM.

Problem/Ansatz: Hallo zusammen,

ich verzweifle etwas an obiger Aufgabe. Zunächst weiß ich bei a) nicht, wie ich die die Bildpunkte korrekt konstruieren kann. Ich habe angefangen mit einem normalen Koordinatensystem, wo ich die Achse eingetragen habe, sowie den Bildpunkt der uns bereits gegeben ist. Daraufhin habe ich auch (2,0) und (4,1) miteinander verbunden. Nun weiß ich allerdings nicht, wie ich die anderen beiden Bildpunkte konstruieren kann.

Bei b) stehe ich auch komplett auf dem Schlauch. Kann mir hier vielleicht zunächst jemand erklären, was es mit dem φ(x) = t + xM auf sich hat? Kann ich damit die Bildpunkte direkt bestimmen, wenn ich x gegeben hätte?

Ich danke euch bereits vielmals für eure Hilfe.

Liebe Grüße

Comments

L ist Fixpunktgerade und Bildpunkte werden wie folgt konstruiert :

Damit wird t = (6 , 3) und M = \( \begin{pmatrix} -1 & -1 \\ -2 & 0 \end{pmatrix} \)

---

Hi,

kannst du mir erklären, was du in diesem Fall gemacht hast? Ich sehe das du den Bildpunkt x über die doppelte Länge dargestellt hast. In der Klausur hätten wir aber theoretisch nur ein Geodreieck zur Verfügung und sollen nicht ausmessen. Was muss ich in diesem Fall dann tun?

Vielen Dank für deine Hilfe!

---

Hm,

da hab ich was anderes, denn

M (2,0)^T + t_0 = (8,-1)^T ?

Muttu transponieren?

---

Was muss ich in diesem Fall dann tun?

Gleichwertige Alternative (falls nicht xa || L ist) :

---

Muttu transponieren?

Nein (hoffe, dass WS das auch liest).

---

er liest es!

@hj: Deine Variante ist richtig. Du hast wahrscheinlich als einziger die Aufgabenestellung GANZ genau gelesen ;-)

... (2 × 2)-Matrix M mit φ(x) = t + xM.

rechnet der Dozent doch glatt mit Zeilenvektoren !!

---

Ajee,

mit Brille wäre das nicht passiert - dann überschreib ich fürs Archiv die Aufgabenstellung   ;-)

Answer 1

Hallo,

Willkommen in der Mathelounge!

Ich bin mir nicht im Klaren, was das \(AG(2,\,R)\) bedeuten soll. Deshalb ist folgende Antwort nur unter Vorbehalt korrekt.

Weiter gehen ich davon aus, dass Punkte auf der gegebenen Achse \(L\) durch die affine Abbildung wieder auf sich selbst abgebildet werden. Grundsätzlich könnten sie auch auf andere Punkte aber auf dieselbe Achse abgebildet werde, aber das macht die Sache kompliziert und mehrdeutig.

Mit den oben beschriebenen Voraussetzungen kann man nun folgende Konstruktion bauen:

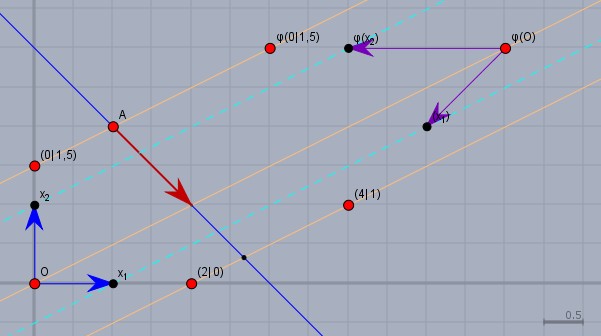
Die gegebenen Punkte und die Achse \(L\) in ein Koordinatensystem einzuzeichnen hast Du schon gemacht. Weiter hast Du den Punkt (2|0) mit seinem Bildpunkt (4|1) verbunden. Die Achse \(L\) (blau) teilt diese Strecke im Verhältnis \(1 \div 2\) .

a) Konstruieren Sie die Bildpunkte von (0, 0) und (0, 3/2 ).

Nun zeichne Parallelen zu dieser Strecke (hellbraun) durch die Punkt (0|0) und (0|1,5). 'Reflektiere' dann diese beiden Punkten auf je ihrer Parallelen wieder im Verhältnis \(1\div 2\) auf die andere Seite von \(L\). Ablesen kann man dann$$\varphi\begin{pmatrix}0& 0\end{pmatrix} = \begin{pmatrix}6& 3\end{pmatrix} \\ \varphi\begin{pmatrix}0& 1,5\end{pmatrix} = \begin{pmatrix}3& 3\end{pmatrix}$$

b) Berechnen Sie t ∈ R und eine (2 × 2)-Matrix M mit φ(x) = t + xM.

Für \(t\) gilt \(t = \varphi\begin{pmatrix} 0& 0\end{pmatrix}\) - also ist$$t = \begin{pmatrix}6& 3\end{pmatrix}$$Die Zeilenvektoren der Matrix \(M\) sind die Bilder der Einheitsvektoren. Wobei (Achtung!) die Bilder der Vektoren bezogen auf das Bild des Ursprungs sind. Das Bild des Ursprungs ist \(t=\)(6|3). Demnach sind die Zeilenvektoren die lila Vektoren im Bild oben. Abgelesen:$$M = \begin{pmatrix} -1 & -1\\ -2 & 0\end{pmatrix}$$Rechnen kan man das auch, aber so ist es einfacher ;-)

Falls Du noch Fragen hast, so melde Dich bitte.

Gruß Werner

Comments

Noch 'ne Bemerkung:

Das ganze beruht darauf, dass Geraden nach einer affinen Abbildung wieder zu Geraden werden und die Bilder von zwei parallelen Geraden sind wieder zueinander parallel.

---

ich habe meine Antwort nochmal korrigiert! Beachte bitte, dass Ihr anscheinend mit Zeilen- statt Spaltenvektoren rechnet. Das ist zwar IMHO nicht üblich, aber völlig korrekt.

---

Hallo Werner,

schon mal vielen Dank für deine und eure Hilfe! Das Konstruieren fällt mir so gar nicht mehr schwer.

Mein Dozent ist für sich selber nicht einig, ob er Zeilen- oder Spaltenvektoren nutzen möchte. Das ist eher Tagesform abhängig.

Zu der Aufgabe b) habe ich allerdings noch fragen. Wieso ist zum einen t=(6,3)? Ist t immer das Bild des Ursprungs?

Und wie könnte ich beides berechnen? Also zum einen t und zum anderen die Matrix? Das würde mich noch interessieren.

Vielen Dank :)

---

Mein Dozent ist für sich selber nicht einig, ob er Zeilen- oder Spaltenvektoren nutzen möchte. Das ist eher Tagesform abhängig.

Oh je! genau dies sollte man tunlichst sein lassen. Das verwirrt doch bloß. Entweder macht man das eine oder das andere. Ich weiteren benutze ich die Zeilenschreibweise ...

Wieso ist zum einen t=(6,3)? Ist t immer das Bild des Ursprungs?

Ja - Der Ursprung hat die Koordinaten \(\begin{pmatrix}0& 0\end{pmatrix}\). Setze das doch in die affine Abbildung ein:$$\varphi\begin{pmatrix}0& 0\end{pmatrix} = t + \begin{pmatrix}0& 0\end{pmatrix}\cdot M = t$$kann also nur \(t\) sein.

Und wie könnte ich beides berechnen? Also zum einen t und zum anderen die Matrix?

das macht man (besser ich) mit homogenen Koordinaten. Homogene Koordinaten zeichnen sich dadurch aus, dass sie noch über eine weitere Dimension verfügen. Dazu hängt man hinter jede Position noch eine \(1\) und hinter jede 'Richtung' eine \(0\).

Also wenn gilt$$\varphi\begin{pmatrix} 2& 0 \end{pmatrix} = \begin{pmatrix} 4& 1 \end{pmatrix}$$dann sieht das in homogenen Koordinaten so aus:$$\varphi\begin{pmatrix} 2& 0& {\color{blue}1} \end{pmatrix} = \begin{pmatrix} 4& 1& {\color{blue}1} \end{pmatrix}$$Warum man das so macht, wird deutlich, wenn man es auf die affine Abbildung anwendet. Aus$$\varphi\begin{pmatrix} x \end{pmatrix} =  xM + t$$wird$$\varphi\begin{pmatrix} x& {\color{blue}1} \end{pmatrix} = \begin{pmatrix} xM + t& {\color{blue}1} \end{pmatrix}= \begin{pmatrix} x& {\color{blue}1} \end{pmatrix} \begin{pmatrix} M& {\color{blue}0}\\t& {\color{blue}1} \end{pmatrix}=x_H \cdot M_H$$damit wird aus der affinen Abbildung eine lineare Abbildung mit einer Vektor-Matrix-Multiplikation.

Jetzt wählt man zwei Positionen auf \(L\), von denen man ja weiß, dass sie auf sich selbst abgebildet werden und zusätzlich die gegeben Position (2|0). Es gilt doch:$$\begin{pmatrix} 4& 1& {\color{blue}1} \end{pmatrix} = \varphi\begin{pmatrix} 2& 0& {\color{blue}1} \end{pmatrix} = \begin{pmatrix} 2& 0& {\color{blue}1} \end{pmatrix} \cdot M_H\\ \begin{pmatrix} 1& 2& {\color{blue}1} \end{pmatrix} = \varphi\begin{pmatrix} 1& 2& {\color{blue}1} \end{pmatrix} = \begin{pmatrix} 1& 2& {\color{blue}1} \end{pmatrix} \cdot M_H\\ \begin{pmatrix} 3& 0& {\color{blue}1} \end{pmatrix} = \varphi\begin{pmatrix} 3& 0& {\color{blue}1} \end{pmatrix} = \begin{pmatrix} 3& 0& {\color{blue}1} \end{pmatrix} \cdot M_H$$und diese drei Gleichungen schreibt man nun ausführlich in Matrixform hin:$$\begin{pmatrix} 4 & 1& 1 \\ 1 & 2& 1 \\ 3& 0& 1 \end{pmatrix} = \begin{pmatrix} 2& 0& 1\\1& 2& 1 \\ 3& 0& 1\end{pmatrix}\cdot M_H$$und nun kann man \(M_H\) berechnen, indem man die Gleichung von links mit der Inversen der Matrix auf der rechten Seite multipliziert$$\implies M_H= \begin{pmatrix}-1& -1& {\color{blue}0}\\ -2& 0& {\color{blue}0} \\ 6& 3&  {\color{blue}1}\end{pmatrix}$$Nun kannst Du links oben die 2x2-Matrix \(M\) und in der dritten Zeile den Vektor \(t\) ablesen. In der dritten Spalte stehen nur wieder die homogenen Koordinaten (blau markiert).

Ich schließe nicht aus, dass es mit der hier gegebene Achse \(L\) zumindest rechentechnisch einfachere Methoden gibt. Aber da fehlt mir aktuell die Zeit, mir diese zu überlegen.

---

Oh je! genau dies sollte man tunlichst sein lassen. Das verwirrt doch bloß.

Wenn er es denn überhaupt macht.
Es ist durchaus üblich, die Koordinaten des Punktes eines affinen Raumes zeilenweise, die der Vektoren des zugehörigen Vektorraumes spaltenweise zu schreiben, und zwar genau deshalb, um ein klares Unterscheidungsmerkmal zu haben und mögliche Verwirrung zu vermeiden.