Hallo 123vier.
Anwendung des Newtonverfahrens:
\( \begin{array}{l}f(x)=\frac{1}{\pi} \int \cos (x \sin t-t) d t \\ f^{\prime}(x)=-\frac{1}{\pi} \int \sin (x \cdot \sin t-t) \cdot \sin t d t\end{array} \)
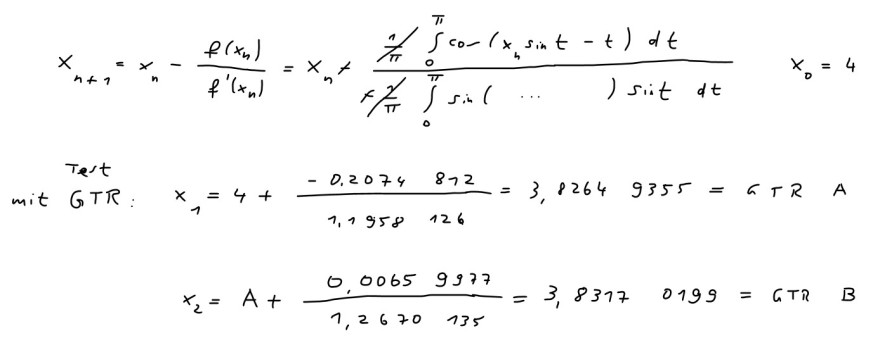
Das funktioniert also schon mal. Jetzt brauchen wir ein numerisches Verfahren zur Berechnung der Integrale.
https://de.wikipedia.org/wiki/Trapezregel
Es spricht nichts dagegen, die beiden Integrale mit der zusammengesetzten Sehnentrapezformel
\( T^{(n)}(f)=h\left(\frac{1}{2} f(a)+\frac{1}{2} f(b)+\sum \limits_{i=1}^{n-1} f(a+i h)\right) \)
zu berechnen.
„Meine Frage zu dieser Aufgabe ist, nachdem ich die Klausur geschrieben habe, einfach nur, ob es sinnvoll ist, das Trapezverfahren und danach das Newtonverfahren zu verwenden. Da ich am Montag in die Einsicht gehe, muss ich irgendwie dafür argumentieren können.“
Also: Umgekehrt: Zuerst das Newtonverfahren für die Nullstellenbestimmung und dann das Trapezverfahren für die Ermittlung der beiden beteiligten Integrale.
Das Newtonverfahren führt schneller zum Ziel als das Intervallhalbierungsverfahren, also ist dies eine gute Lösung. Die Bedingung f‘(x) ≠ 0 ist erfüllt.
Das Trapezverfahren ist ein einfaches und anschauliches Verfahren. Es ist das einfachste aus der Reihe der Newton-Cotes-Formeln. Siehe
https://de.wikipedia.org/wiki/Newton-Cotes-Formeln
Also liegst du richtig mit deiner Lösung in der Klausur.
