Leuchtkugel Aufgabe (Vektoren)

Question

Text erkannt:

14 Eine Leuchtkugel fliegt vom Punkt \( P(4|0| 0) \) geradlinig in Richtung des Punktes \( Q(0|0| 3) \). Eine zweite Leuchtkugel startet gleichzeitig vom Punkt \( R(0|3| 0) \) und fliegt geradlinig in Richtung des Punktes \( T(0|0| 7) \). Beide Kugeln fliegen gleich schnell. Wie weit sind die Kugeln zu dem Zeitpunkt voneinander entfernt, bei dem die erste Kugel den Punkt Q erreicht?

Ich muss diese Aufgabe lösen. Ich habe die Flugbahnen schon bestimmt jedoch weißlich nicht wie es weitergeht. Ich ne muss glaube ich die Aussage, dass ", beide kugeln gleich Schnell fliegen " noch beachten! Ich weiß jedoch nicht wie

-

Comments

Ich habe die Flugbahnen schon bestimmt

Es wäre zweckmäßig, Deine Ergebnisse hier aufzuschreiben...

Answer 1

PQ = [0, 0, 3] - [4, 0, 0] = [-4, 0, 3]

|PQ| = 5

Die erste Kugel fliegt also 5 LE weit. Genau diese Strecke muss auch die 2. Kugel zurücklegen.

RT = [0, 0, 7] - [0, 3, 0] = [0, -3, 7]

T' = [0, 3, 0] + 5·[0, -3, 7]/|[0, -3, 7]| = [0, 3 - 15/58·√58, 35/58·√58]

Der Abstand der Kugeln beträgt damit etwa.

|QT'| = 1.899 LE

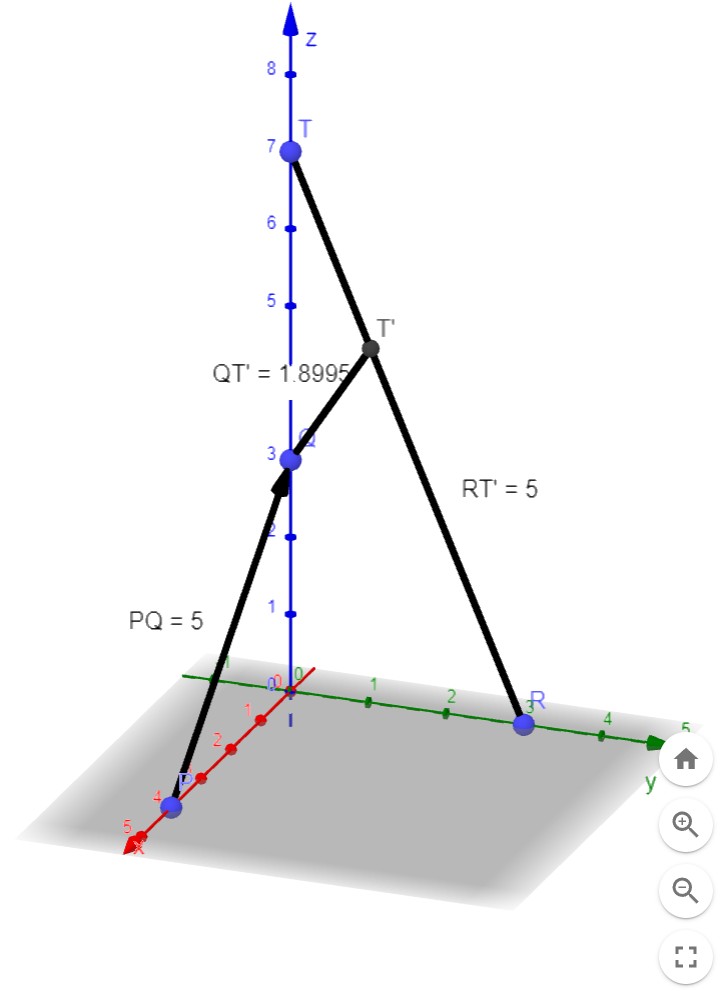
Skizze

Answer 2

dass ", beide kugeln gleich Schnell fliegen " noch beachten! Ich weiß jedoch nicht wie

Gleichschnell bedeutet, dass die Kugeln in der gleichen Zeit, die gleiche Strecke zurücklegen. Wenn man Flugbahnen hat, dann wird durch den Richtungsvektor die Richtung, aber gleichzeitig auch die Geschwindigkeit angegeben. Je nachdem, wie lang der Richtungsvektor ist. Der Parameter gibt dann bspw. die Zeit in Sekunden an.

Du kannst hier also mit demselben Parameter bei beiden Flugbahnen arbeiten, wenn du die Richtungsvektoren so aufstellst, dass sie die gleiche Länge haben. Mit Hilfe des Parameters kannst du dann bestimmen, wann die erste Kugeln beim Punkt \(Q\) ist. Mit demselben Parameter kannst du dann aber den Ort der zweiten Kugel bestimmen, da die Kugeln ja gleichzeitig losfliegen.