Bestimme den Grenzwert von: lim x- 0 (6(ln(1+x)+(ln1+2x))/(x^2)

Question

Aufgabe:

Bestimme den Grenzwert von: lim x->0 (6(ln(1+x)+ln(1+2x))/(x^2)

Problem/Ansatz:

Da der Grenzwert [0/0] ist, kann man L´Hospital anwenden.

Nach L´Hospital ergibt sich: (8+14x)/(2x(2x^2+3x+1)). Der Grenzwert ist hier [8/0], aber durch 0 ist nicht definiert.
Stehe ich auf dem Schlauch oder existiert der Grenzwert dann nicht?

Hilfe dringend benötigt.

Comments

Wäre vielleicht gut, zunächst die Klammern korrekt zu setzen, und zu überprüfen, ob die Aufgabe im Original tatsächlich so lautet.

Oder einfach einen Screenshot der Aufgabe hochladen.

---

lim x->0 \( \frac{6(ln(1+x)+ln(1+2x))}{x^2} \) = [\( \frac{0}{0} \)]

= lim x->0 \( \frac{8+14x}{2x(2x^2+3x+1)} \) = [\( \frac{8}{0} \)]

besser?

Wir müssen den grenzwert mit l´hospital bestimmen.

---

Ein praktischer Hinweis: Die Ablitung des Zählers braucht nicht zusammengefasst werden. Man kann sie direkt auswerten.

Answer 1

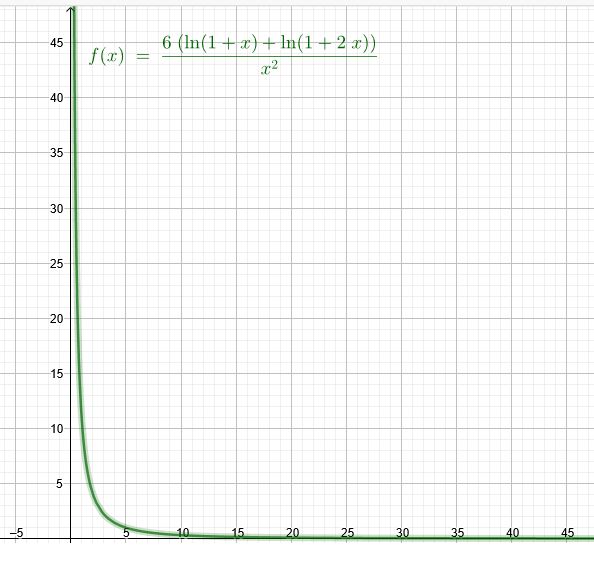
\( \lim\limits_{x\to 0}\frac{6(ln(1+x)+ln(1+2x))}{x^2} \)

----------------------------------------

\(Z=6[ln(1+x)+ln(1+2x)]\)

\(Z'=6[\frac{1}{1+x}+\frac{2}{1+2x}]=\frac{6}{1+x}+\frac{12}{1+2x}=\frac{18+24x}{(1+x)(1+2x)}\)

\(N=x^2\)

\(N'=2x\)

\( \lim\limits_{x\to 0}\frac{6(ln(1+x)+ln(1+2x))}{x^2}=\lim\limits_{x\to 0}\frac{18+24x}{2x(1+x)(1+2x)}=∞\)

Comments

\(\lim\limits_{x\to 0}...=\infty\) stimmt nicht.

---

Es wäre günstig, wenn man sieht, dass der Nenner bei x = 0 eine Nullstelle mit Vorzeichenwechsel hat.

Answer 2

Du hast fast richtig gerechnet. Der Grenzwert existiert nicht, dazu muss man aber genauer hinschauen: \(\lim\limits_{x\to 0+} \frac{6(4x+3)}{2x(2x^2+3x+1)}=\infty\) und \(\lim\limits_{x\to 0-} \frac{6(4x+3)}{2x(2x^2+3x+1)}=-\infty\).

Das sind auch die entsprechenden Grenzwert für die Ausgangsfunktion, denn die Regel von l'H gilt auch für einseitige Grenzwerte.

Comments

\(\lim\limits_{x\to 0+} \frac{8+14x}{2x(2x^2+3x+1)}=\infty\)

\(\lim\limits_{x\to 0-} \frac{8+14x}{2x(2x^2+3x+1)}=-\infty\)

Hier stimmen die Zähler nicht!

---

Danke, ist korrigiert.