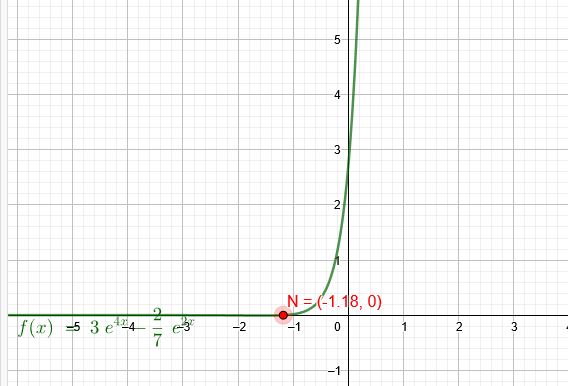
Lösungsweg mit Ausklammern:
\(3e^{4x}-\frac{2}{7}e^{2x}=0\)
\(e^{2x}(3e^{2x}-\frac{2}{7})=0\)
\(e^{2x}≠0\)
\(3e^{2x}-\frac{2}{7}=0\)
\(e^{2x}=\frac{2}{21}\)
\(2x\cdot \ln(e)=\ln(\frac{2}{21})\) mit \(\ln(e)=1)\):
\(x=\frac{\ln(\frac{2}{21})}{2}≈-1.18\)