Aufgabe:
Bei b) wäre meine Frage wie man auf 124740 kommt bei a) ist das Ergebnis 48828125.
Problem/Ansatz:
Was rechnet man bei b) genau? 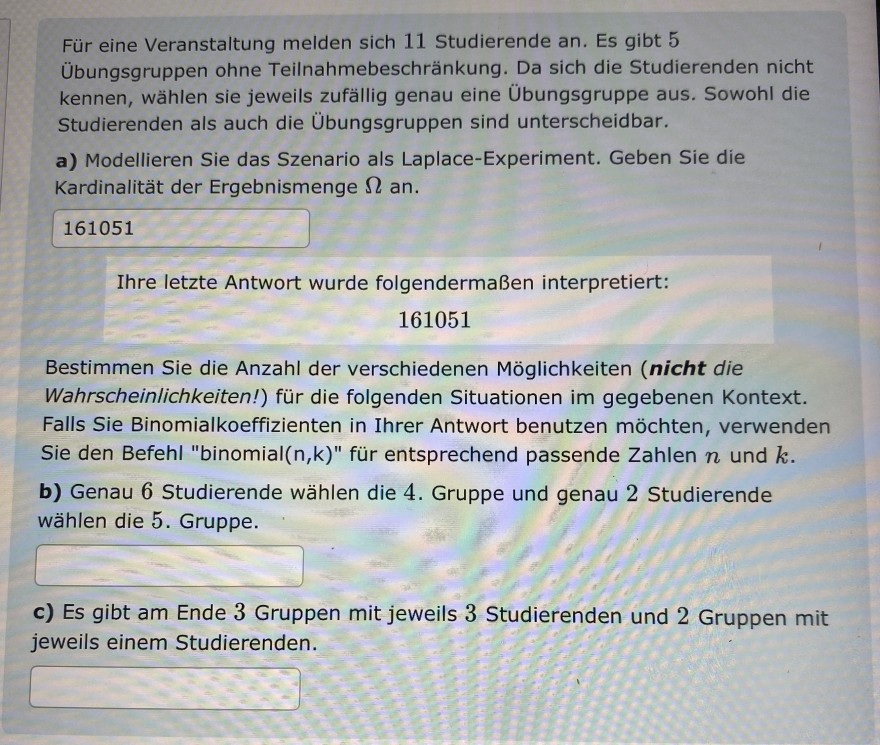
Text erkannt:
Für eine Veranstaltung melden sich 11 Studierende an. Es gibt 5 Übungsgruppen ohne Teilnahmebeschränkung. Da sich die Studierenden nicht kennen, wählen sie jeweils zufällig genau eine Übungsgruppe aus. Sowohl die Studierenden als auch die Übungsgruppen sind unterscheidbar.
a) Modellieren Sie das Szenario als Laplace-Experiment. Geben Sie die Kardinalität der Ergebnismenge \( \Omega \) an.
\( 161051 \)
Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( 161051 \)
Bestimmen Sie die Anzahl der verschiedenen Möglichkeiten (nicht die Wahrscheinlichkeiten!) für die folgenden Situationen im gegebenen Kontext. Falls Sie Binomialkoeffizienten in Ihrer Antwort benutzen möchten, verwenden Sie den Befehl "binomial \( (\mathrm{n}, \mathrm{k}) \) " für entsprechend passende Zahlen \( n \) und \( k \).
b) Genau 6 Studierende wählen die 4 . Gruppe und genau 2 Studierende wählen die 5 . Gruppe.
c) Es gibt am Ende 3 Gruppen mit jeweils 3 Studierenden und 2 Gruppen mit jeweils einem Studierenden.