bestimmen Sie diejenigen von a,für die diese Tangente eine positive Steigung hat und zudem die x-achse in einem …

Question

Aufgabe:

Angabe: Gegeben sind die in IR definierten Funktionen fa mit fa(x)=a • e ^-x +3 und a ~ IR\{0}.

Frage:

Betrachtet wird die Tangente an den Graphen von fa im Punkt (0/fa (0)). bestimmen Sie diejenigen von a,für die diese Tangente eine positive Steigung hat und zudem die x-achse in einem Punkt schneidet,dessen x - koordinate größer als ½ ist.

Problem/Ansatz:

Wie rechnet man das? Lösungsansatz

Comments

bestimmen Sie diejenigen von a

diejenigen was von a? Werte?

Wie rechnet man das?

Bilde die Ableitung der Funktion.

---

Ich habe keine Werte. Eine ableitung habe ich.

---

Ich habe nicht nach Werten gefragt. Ich wollte fragen, ob "Werte" das fehlende Wort ist. Was ist Deine Ableitung?

Answer 1

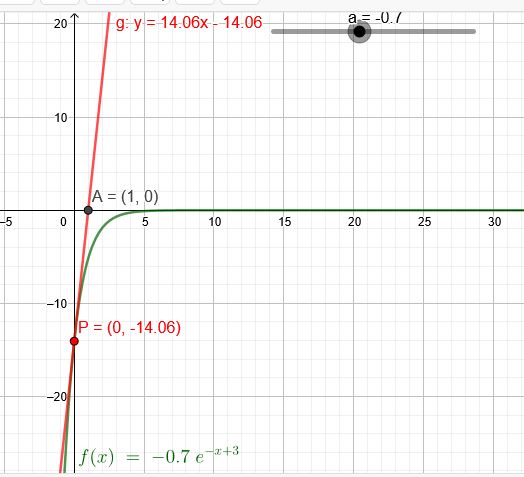
\(f_a(x)=a\cdot  e^{-x+3} \)

\(f_a(0)=a\cdot e^{3} \)

\(f_a'(x)=a\cdot e^{-x+3} \cdot (-1) \)

\(f_a'(0)=-a\cdot e^{3}  \)

Tangente durch P\((0|a\cdot e^{3})\) mit der Steigung \(f_a'(0)=-a\cdot e^{3}  \)

\( \frac{y-a\cdot e^{3} }{x-0}=-a\cdot e^{3} \)

Schnitt der Tangente mit der x-Achse (\(y=0\))

\( \frac{-a\cdot e^{3} }{x}=-a\cdot e^{3} \)

\(x=1\)

Comments

Danke...hab ich jetzt verstanden. Sie haben mir sehr weitergeholfen.

Answer 2

Ich vermute die + 3 steht nicht im Exponenten

fa(x) = a·e^(- x) + 3
fa'(x) = - a·e^(- x)

Steigung der Tangente

f'(0) = - a > 0 → a < 0

Nullstelle der Tangente

t(x) = fa'(0)·x + fa(0) = - a·x + a + 3 = 0 → x = (a + 3)/a > 1/2 → a < - 6 ∨ a > 0

Damit müsste a < -6 sein.

Comments

Danke für die Lösung. Habe ich verstanden. Sie konnten mir sehr weiterhelfen.

---

Beachte, dass ich eine andere Antwort habe als Moliets.

Steht die + 3 bei der Funktion im Exponenten oder nicht. Davon ist es abhängig, welche Antwort dir weiterhilft und welche nicht.

---

Deine ist richtig. !!!!