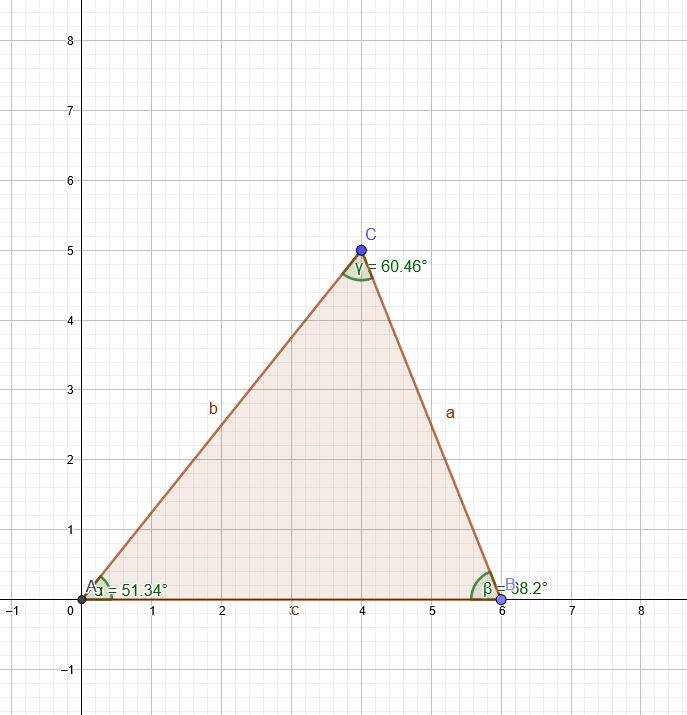
Die Ecken des allgemeinen Dreiecks werden gegen den Uhrzeigersinn mit den Buchstaben A, B und C beschriftet.
Die Strecke zwischen A und B wird c genannt ( gegenüber vom Punkt C).
Die Strecke zwischen B und C wird a genannt ( gegenüber vom Punkt A).
Die Strecke zwischen A und C wird b genannt ( gegenüber vom Punkt B).
Der Winkel bei A erhält den griechischen Buchstaben α (alpha).
Der Winkel bei B erhält den griechischen Buchstaben β (beta).
Der Winkel bei C erhält den griechischen Buchstaben γ (gamma).