6) Der Querschnitt eines Kanals ist ein Rechteck mit unten angesetztem Halbkreis. Wählen Sie die Maße dieses Rechtecks so, dass bei gegebenem Umfang U des Querschnitts des Kanals sein Flächeninhalt möglichst groß wird.
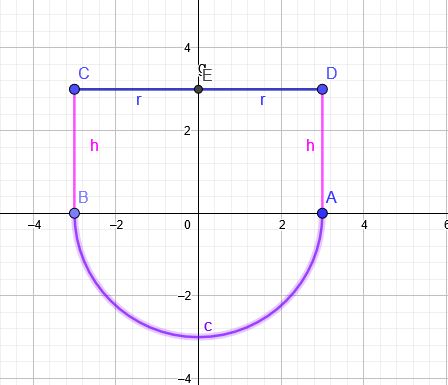
\(A(r,h)=2 r h+0,5 r^2 π\) soll maximal werden.
NB:
\(U =2r+2h+r π \) Auflösung nach h:
\(h = \frac{1}{2}U-\frac{r }{2} π-r \)
\(A(r)=2 r (\frac{1}{2}U-\frac{r }{2} π-r )+0,5 r^2 π\)
\(A'(r)=2 \cdot (\frac{1}{2}U-\frac{r }{2} π-r )+2 r \cdot (-0,5π-1)+rπ\)
\(2 \cdot (\frac{1}{2}U-\frac{r }{2} π-r )+2 r \cdot (-0,5π-1)+rπ=0\)
Nun nach r auflösen....